Intro
Discover 5 Riemann obituaries, exploring Bernhard Riemanns legacy in mathematics, geometry, and topology, influencing modern calculus, differential equations, and number theory research.
The life and work of Bernhard Riemann, a renowned German mathematician, have had a profound impact on the development of mathematics and physics. Riemann's contributions to differential geometry, number theory, and mathematical physics have left a lasting legacy, influencing generations of mathematicians and scientists. In this article, we will delve into the significance of Riemann's work, exploring his most notable achievements and their far-reaching implications.
Riemann's work on differential geometry, in particular, has had a profound impact on our understanding of space and time. His development of Riemannian geometry, which describes the properties of curved spaces, has been instrumental in shaping our understanding of the universe. From the curvature of space-time in Einstein's theory of general relativity to the geometry of black holes, Riemann's ideas have played a central role in advancing our knowledge of the cosmos. Moreover, his work on the Riemann hypothesis, a conjecture about the distribution of prime numbers, remains one of the most famous unsolved problems in mathematics, continuing to inspire research and innovation.
The significance of Riemann's work extends beyond the realm of mathematics, with far-reaching implications for physics, engineering, and computer science. His ideas have influenced the development of theories such as quantum mechanics and string theory, and have been applied in fields such as computer graphics, medical imaging, and signal processing. As we continue to push the boundaries of human knowledge, Riemann's contributions remain a vital foundation, inspiring new discoveries and advancements.
Riemann's Life and Work
Riemann was born in 1826 in Breselenz, a small village in the Kingdom of Hanover. His early life was marked by a passion for mathematics, which was encouraged by his father, a Lutheran pastor. Riemann's academic career took him to the University of Göttingen, where he studied mathematics and philosophy, eventually earning his Ph.D. under the supervision of Carl Friedrich Gauss. Riemann's dissertation, which explored the foundations of geometry, laid the groundwork for his future research and established him as a rising star in the mathematical community.
Key Contributions
Riemann's work can be divided into several key areas, each of which has had a significant impact on the development of mathematics and physics. Some of his most notable contributions include: * The development of Riemannian geometry, which describes the properties of curved spaces * The Riemann hypothesis, a conjecture about the distribution of prime numbers * The theory of Riemann surfaces, which provides a framework for understanding the properties of complex functions * The development of the Riemann integral, which provides a rigorous foundation for calculusRiemannian Geometry

Riemannian geometry, which was introduced by Riemann in his famous lecture "On the Hypotheses which lie at the Foundations of Geometry," provides a framework for understanding the properties of curved spaces. This theory, which describes the curvature of spaces in terms of the Riemann tensor, has been instrumental in shaping our understanding of the universe. From the curvature of space-time in Einstein's theory of general relativity to the geometry of black holes, Riemannian geometry has played a central role in advancing our knowledge of the cosmos.
Applications of Riemannian Geometry
The applications of Riemannian geometry are diverse and far-reaching, with implications for fields such as physics, engineering, and computer science. Some of the key applications of Riemannian geometry include: * The theory of general relativity, which describes the curvature of space-time in terms of the Riemann tensor * The geometry of black holes, which is described using Riemannian geometry * Computer graphics, where Riemannian geometry is used to create realistic models of curved surfaces * Medical imaging, where Riemannian geometry is used to reconstruct images of the bodyThe Riemann Hypothesis

The Riemann hypothesis, which was first proposed by Riemann in 1859, is a conjecture about the distribution of prime numbers. This hypothesis, which states that all non-trivial zeros of the Riemann zeta function lie on a vertical line in the complex plane, has far-reaching implications for number theory and mathematics as a whole. Despite considerable effort, the Riemann hypothesis remains one of the most famous unsolved problems in mathematics, with a solution offering a $1 million prize from the Clay Mathematics Institute.
Implications of the Riemann Hypothesis
The implications of the Riemann hypothesis are diverse and far-reaching, with potential applications in fields such as cryptography, coding theory, and numerical analysis. Some of the key implications of the Riemann hypothesis include: * A deeper understanding of the distribution of prime numbers, which is essential for many applications in mathematics and computer science * Improved algorithms for testing primality and factoring large numbers, which has significant implications for cryptography and coding theory * A better understanding of the properties of the Riemann zeta function, which is a fundamental object in number theoryLegacy of Riemann's Work

Riemann's work has had a profound impact on the development of mathematics and physics, influencing generations of mathematicians and scientists. His ideas have shaped our understanding of space and time, and have been instrumental in advancing our knowledge of the universe. From the theory of general relativity to the geometry of black holes, Riemann's contributions have left a lasting legacy, continuing to inspire research and innovation.
Influence on Modern Mathematics and Physics
Riemann's work has had a significant influence on modern mathematics and physics, with implications for fields such as differential geometry, number theory, and mathematical physics. Some of the key areas where Riemann's work has had an impact include: * The development of modern differential geometry, which provides a framework for understanding the properties of curved spaces * The theory of general relativity, which describes the curvature of space-time in terms of the Riemann tensor * The geometry of black holes, which is described using Riemannian geometry * The development of modern number theory, which is essential for many applications in mathematics and computer scienceRiemann Image Gallery







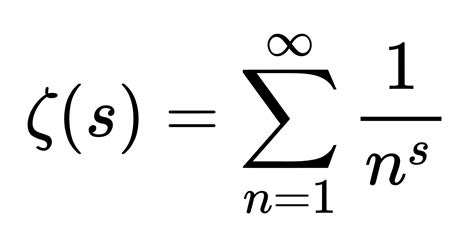

As we reflect on the life and work of Bernhard Riemann, it is clear that his contributions to mathematics and physics have left a lasting legacy. His ideas have shaped our understanding of space and time, and have been instrumental in advancing our knowledge of the universe. We invite you to share your thoughts on Riemann's work and its significance, and to explore the many resources available for learning more about this fascinating topic. Whether you are a mathematician, physicist, or simply someone interested in learning more about the world around us, Riemann's work is sure to inspire and educate.
