Intro
Boost your data analysis skills with our expert guide on using a sample size calculator in Excel. Learn 5 practical ways to apply this tool, including hypothesis testing, confidence intervals, and margin of error. Improve your statistical accuracy and make informed decisions with our comprehensive tutorial on sample size calculation in Excel.
Calculating the right sample size is a crucial step in any research study or experiment. A sample size that is too small may not provide reliable results, while a sample size that is too large may be wasteful and unnecessary. Fortunately, there are tools available to help you determine the right sample size for your study, including sample size calculators in Excel.
In this article, we will explore five ways to use sample size calculators in Excel, including determining the sample size for a confidence interval, estimating the sample size for a hypothesis test, calculating the sample size for a regression analysis, determining the sample size for a survey, and estimating the sample size for a pilot study.
Determining the Sample Size for a Confidence Interval
A confidence interval is a statistical tool used to estimate a population parameter. To determine the sample size for a confidence interval, you need to know the desired margin of error, the confidence level, and the standard deviation of the population.

To calculate the sample size for a confidence interval in Excel, you can use the following formula:
n = (Z^2 * σ^2) / E^2
Where:
- n = sample size
- Z = Z-score corresponding to the desired confidence level
- σ = standard deviation of the population
- E = margin of error
For example, if you want to estimate the average height of a population with a margin of error of 2 inches and a confidence level of 95%, you can use the following values:
- Z = 1.96 (corresponding to a 95% confidence level)
- σ = 10 (standard deviation of the population)
- E = 2 (margin of error)
Plugging these values into the formula, you get:
n = (1.96^2 * 10^2) / 2^2 n = 96.04
Therefore, you need a sample size of at least 96 to estimate the average height of the population with a margin of error of 2 inches and a confidence level of 95%.
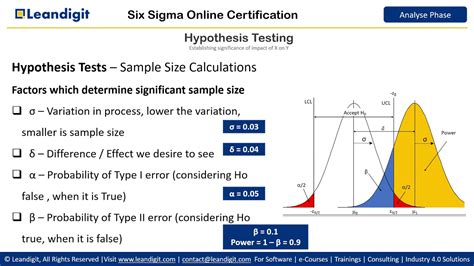
Estimating the Sample Size for a Hypothesis Test
A hypothesis test is a statistical tool used to test a null hypothesis against an alternative hypothesis. To estimate the sample size for a hypothesis test, you need to know the desired power, the effect size, and the significance level.

To calculate the sample size for a hypothesis test in Excel, you can use the following formula:
n = (Z^2 * σ^2) / (μ1 - μ0)^2
Where:
- n = sample size
- Z = Z-score corresponding to the desired power
- σ = standard deviation of the population
- μ1 = mean of the alternative hypothesis
- μ0 = mean of the null hypothesis
For example, if you want to test the null hypothesis that the average height of a population is 65 inches against the alternative hypothesis that the average height is 70 inches, with a significance level of 0.05 and a power of 0.8, you can use the following values:
- Z = 0.842 (corresponding to a power of 0.8)
- σ = 10 (standard deviation of the population)
- μ1 = 70 (mean of the alternative hypothesis)
- μ0 = 65 (mean of the null hypothesis)
Plugging these values into the formula, you get:
n = (0.842^2 * 10^2) / (70 - 65)^2 n = 175.84
Therefore, you need a sample size of at least 176 to test the null hypothesis against the alternative hypothesis with a significance level of 0.05 and a power of 0.8.
Calculating the Sample Size for a Regression Analysis
A regression analysis is a statistical tool used to model the relationship between a dependent variable and one or more independent variables. To calculate the sample size for a regression analysis, you need to know the desired R-squared value, the number of independent variables, and the significance level.

To calculate the sample size for a regression analysis in Excel, you can use the following formula:
n = (Z^2 * σ^2) / (1 - R^2)
Where:
- n = sample size
- Z = Z-score corresponding to the desired significance level
- σ = standard deviation of the dependent variable
- R = desired R-squared value
For example, if you want to estimate the relationship between the average height of a population and the average weight of the population, with a desired R-squared value of 0.8 and a significance level of 0.05, you can use the following values:
- Z = 1.96 (corresponding to a 95% confidence level)
- σ = 10 (standard deviation of the dependent variable)
- R = 0.8 (desired R-squared value)
Plugging these values into the formula, you get:
n = (1.96^2 * 10^2) / (1 - 0.8^2) n = 386.4
Therefore, you need a sample size of at least 387 to estimate the relationship between the average height and the average weight of the population with a desired R-squared value of 0.8 and a significance level of 0.05.
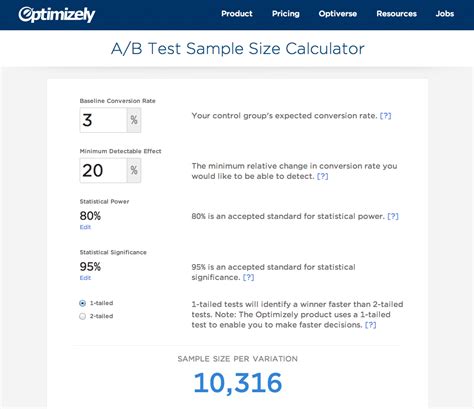
Determining the Sample Size for a Survey
A survey is a statistical tool used to collect data from a sample of respondents. To determine the sample size for a survey, you need to know the desired margin of error, the confidence level, and the population size.

To calculate the sample size for a survey in Excel, you can use the following formula:
n = (Z^2 * σ^2) / (E^2 * (N - 1))
Where:
- n = sample size
- Z = Z-score corresponding to the desired confidence level
- σ = standard deviation of the population
- E = margin of error
- N = population size
For example, if you want to estimate the average opinion of a population on a certain issue, with a margin of error of 3% and a confidence level of 95%, and the population size is 10,000, you can use the following values:
- Z = 1.96 (corresponding to a 95% confidence level)
- σ = 10 (standard deviation of the population)
- E = 3 (margin of error)
- N = 10,000 (population size)
Plugging these values into the formula, you get:
n = (1.96^2 * 10^2) / (3^2 * (10,000 - 1)) n = 1067.11
Therefore, you need a sample size of at least 1068 to estimate the average opinion of the population on the issue with a margin of error of 3% and a confidence level of 95%.
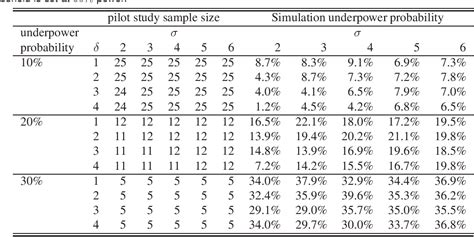
Estimating the Sample Size for a Pilot Study
A pilot study is a small-scale study used to test the feasibility of a larger study. To estimate the sample size for a pilot study, you need to know the desired power, the effect size, and the significance level.

To calculate the sample size for a pilot study in Excel, you can use the following formula:
n = (Z^2 * σ^2) / (μ1 - μ0)^2
Where:
- n = sample size
- Z = Z-score corresponding to the desired power
- σ = standard deviation of the population
- μ1 = mean of the alternative hypothesis
- μ0 = mean of the null hypothesis
For example, if you want to test the null hypothesis that the average height of a population is 65 inches against the alternative hypothesis that the average height is 70 inches, with a significance level of 0.05 and a power of 0.8, you can use the following values:
- Z = 0.842 (corresponding to a power of 0.8)
- σ = 10 (standard deviation of the population)
- μ1 = 70 (mean of the alternative hypothesis)
- μ0 = 65 (mean of the null hypothesis)
Plugging these values into the formula, you get:
n = (0.842^2 * 10^2) / (70 - 65)^2 n = 175.84
Therefore, you need a sample size of at least 176 to test the null hypothesis against the alternative hypothesis with a significance level of 0.05 and a power of 0.8.
We hope this article has provided you with a comprehensive understanding of how to use sample size calculators in Excel for different statistical analyses. Remember to always consult with a statistician or a researcher before conducting any study to ensure that your sample size is sufficient and your results are reliable.
Gallery of Sample Size Calculators
Sample Size Calculator Image Gallery





We hope this article has been informative and helpful in understanding how to use sample size calculators in Excel. If you have any questions or need further clarification, please do not hesitate to ask.
