Sampling Without Replacement Formula Explained Simply

Sampling without replacement is a fundamental concept in statistics, and it's essential to understand the formula behind it. In this article, we'll break down the sampling without replacement formula and explain it in simple terms.

What is Sampling Without Replacement?

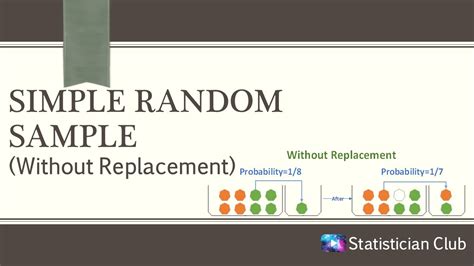
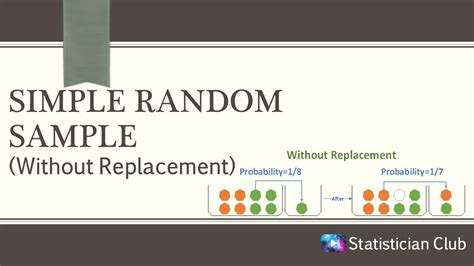
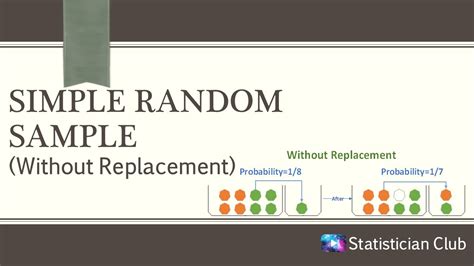
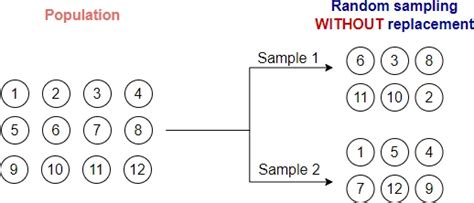
Sampling without replacement is a method of selecting a sample from a population where each member can only be chosen once. This means that once an individual is selected, they are removed from the population, and the remaining members have an equal chance of being selected. This technique is often used in statistical analysis, quality control, and market research.

Why is Sampling Without Replacement Important?

Sampling without replacement is crucial in ensuring that the sample is representative of the population. By not allowing individuals to be selected multiple times, we reduce the risk of bias and ensure that each member of the population has an equal chance of being represented. This method also helps to prevent over-representation of certain individuals or groups, which can lead to inaccurate conclusions.

The Sampling Without Replacement Formula

The sampling without replacement formula is used to calculate the probability of selecting a specific sample from a population. The formula is as follows:

P(S) = (n! / (n-r)!) * (N-r)! / N!

Where:

• P(S) is the probability of selecting the sample
• n is the sample size
• N is the population size
• r is the number of items being selected *! denotes the factorial function (e.g., 5! = 5 * 4 * 3 * 2 * 1)

Breaking Down the Formula

Let's break down the formula to understand what each component represents:

• (n! / (n-r)!) represents the number of ways to choose r items from a sample of size n. This is calculated using the combination formula.
• (N-r)! represents the number of ways to arrange the remaining N-r items in the population.
• N! represents the total number of ways to arrange all N items in the population.

Example of Sampling Without Replacement

Suppose we have a population of 100 students, and we want to select a sample of 10 students without replacement. Using the formula, we can calculate the probability of selecting a specific sample:

P(S) = (10! / (10-10)!) * (100-10)! / 100! = (10! / 0!) * (90)! / 100! = 1 * 90! / 100!

This result represents the probability of selecting the specific sample of 10 students from the population of 100.

Advantages and Disadvantages of Sampling Without Replacement

Advantages:

• Ensures that each member of the population has an equal chance of being selected
• Reduces the risk of bias and over-representation
• Provides a more accurate representation of the population

Disadvantages:

• Can be time-consuming and resource-intensive
• May not be suitable for large populations
• Can lead to sampling errors if the sample size is too small

Real-World Applications of Sampling Without Replacement

Sampling without replacement has numerous real-world applications, including:

• Quality control: Manufacturers use sampling without replacement to ensure that their products meet quality standards.
• Market research: Researchers use sampling without replacement to gather data on consumer behavior and preferences.
• Statistical analysis: Statisticians use sampling without replacement to analyze data and make conclusions about a population.

Conclusion

In conclusion, sampling without replacement is a crucial concept in statistics that ensures that each member of the population has an equal chance of being selected. The formula for sampling without replacement is used to calculate the probability of selecting a specific sample from a population. While it has its advantages and disadvantages, sampling without replacement has numerous real-world applications in quality control, market research, and statistical analysis.

Gallery of Sampling Without Replacement

We hope this article has helped you understand the concept of sampling without replacement and its applications. If you have any questions or comments, please feel free to share them below.