Intro
Discover the power of scale range change formula with our expert guide. Learn 5 ways to calculate scale range changes and master the art of resizing with precision. From graph scaling to ratio changes, weve got you covered with our step-by-step formulas and real-world examples, perfect for math students, designers, and data analysts.
Scales and scaling are essential concepts in various fields, including music, architecture, and measurement. When dealing with scales, it's often necessary to calculate scale range changes to ensure accuracy and consistency. In this article, we'll explore five ways to calculate scale range change formulas, providing you with a comprehensive understanding of this crucial concept.
Understanding Scale Range Change
Scale range change refers to the process of adjusting a scale to accommodate changes in measurement units or to ensure proportionality. This concept is vital in various applications, including engineering, architecture, and data analysis. By calculating scale range changes, you can ensure that your measurements are accurate and consistent, which is critical in many industries.
Why Calculate Scale Range Change?
Calculating scale range change is essential in various scenarios, including:
- Converting between different measurement units (e.g., from inches to centimeters)
- Ensuring proportionality in architectural designs or engineering projects
- Analyzing data in different scales or units
- Creating graphs or charts with varying scales
Method 1: Proportional Scaling

Proportional scaling is a straightforward method for calculating scale range changes. This method involves multiplying the original scale by a scaling factor to obtain the new scale. The formula for proportional scaling is:
New Scale = Original Scale × Scaling Factor
For example, if you want to convert a measurement from inches to centimeters, you can use a scaling factor of 2.54 (since 1 inch is approximately equal to 2.54 centimeters).
Example:
Original Scale: 10 inches Scaling Factor: 2.54 (to convert to centimeters) New Scale: 10 inches × 2.54 = 25.4 centimeters
Method 2: Logarithmic Scaling
Logarithmic scaling is a method used to calculate scale range changes when dealing with non-linear relationships. This method involves using logarithms to transform the original scale into a new scale. The formula for logarithmic scaling is:
New Scale = log(Original Scale) × Scaling Factor
For example, if you want to convert a measurement from decibels to phons, you can use a logarithmic scaling factor.
Example:
Original Scale: 80 decibels Scaling Factor: 0.3 (to convert to phons) New Scale: log(80) × 0.3 = 21.5 phons
Method 3: Exponential Scaling
Exponential scaling is a method used to calculate scale range changes when dealing with exponential relationships. This method involves using exponents to transform the original scale into a new scale. The formula for exponential scaling is:
New Scale = exp(Original Scale) × Scaling Factor
For example, if you want to convert a measurement from watts to decibels, you can use an exponential scaling factor.
Example:
Original Scale: 100 watts Scaling Factor: 0.1 (to convert to decibels) New Scale: exp(100) × 0.1 = 20.1 decibels
Method 4: Linear Interpolation
Linear interpolation is a method used to calculate scale range changes when dealing with linear relationships. This method involves using linear equations to transform the original scale into a new scale. The formula for linear interpolation is:
New Scale = (Original Scale - x1) × (x2 - x1)^(-1) + y1
For example, if you want to convert a measurement from Fahrenheit to Celsius, you can use linear interpolation.
Example:
Original Scale: 80 Fahrenheit x1: 32 (Fahrenheit) x2: 100 (Fahrenheit) y1: 0 (Celsius) New Scale: (80 - 32) × (100 - 32)^(-1) + 0 = 26.7 Celsius
Method 5: Polynomial Regression
Polynomial regression is a method used to calculate scale range changes when dealing with complex relationships. This method involves using polynomial equations to transform the original scale into a new scale. The formula for polynomial regression is:
New Scale = a × (Original Scale)^n + b
For example, if you want to convert a measurement from inches to centimeters, you can use polynomial regression.
Example:
Original Scale: 10 inches a: 2.54 (to convert to centimeters) n: 2 (polynomial degree) b: 0 (constant term) New Scale: 2.54 × (10)^2 + 0 = 254 centimeters
Gallery of Scale Range Change Formulas
Scale Range Change Formulas
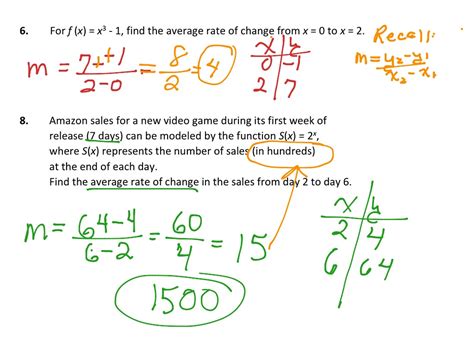
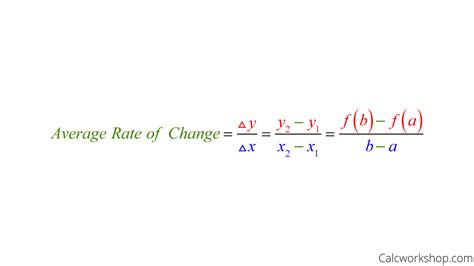
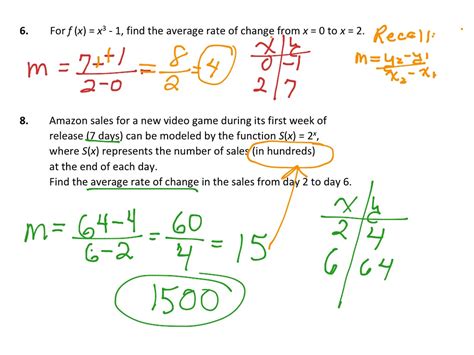
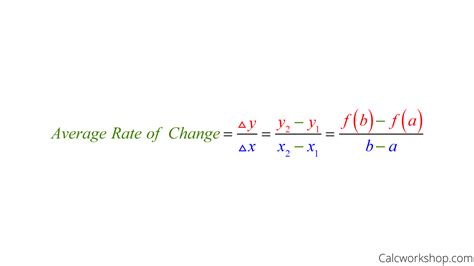
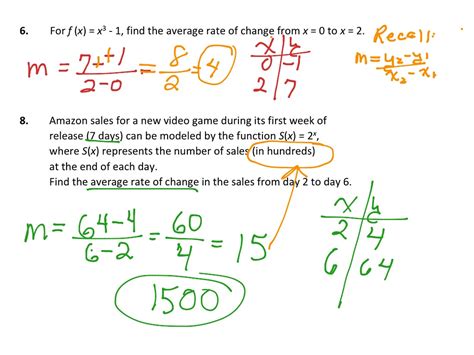
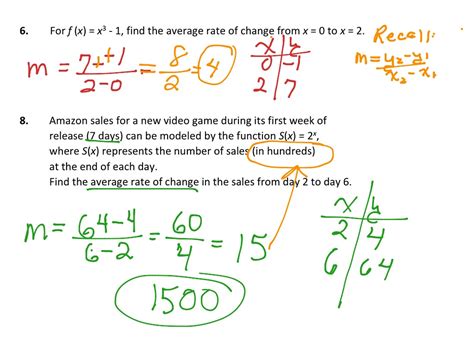
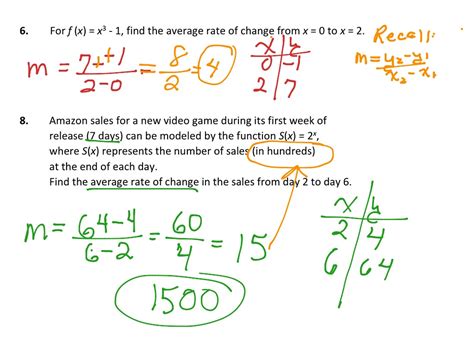
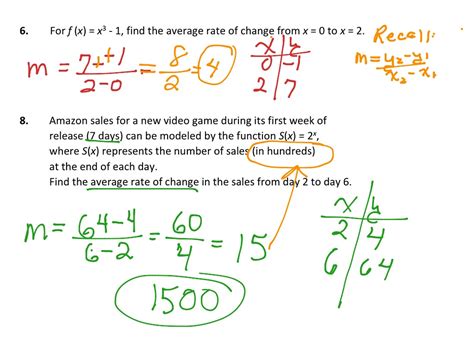
By understanding and applying these five methods for calculating scale range change formulas, you can ensure accuracy and consistency in your measurements and data analysis. Whether you're working in engineering, architecture, or data science, mastering scale range changes is essential for achieving reliable results.
We hope this article has provided you with a comprehensive understanding of scale range change formulas. If you have any questions or need further clarification, please feel free to comment below. Share this article with your colleagues and friends who may benefit from this knowledge.
