Intro
Discover the secrets of the semicircle center of mass and how its calculated. Learn about the formula, derivation, and real-world applications of this fundamental physics concept. Understand the relationship between the semicircles radius, density, and center of mass, and explore examples of its use in engineering and architecture.
The concept of center of mass is a fundamental idea in physics and engineering, and it's essential to understand how it applies to different shapes, including semicircles. In this article, we'll delve into the world of semicircle center of mass, exploring its definition, calculation methods, and practical applications.
What is Center of Mass?
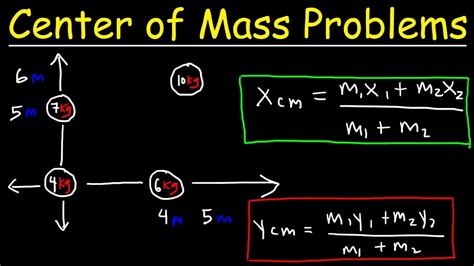
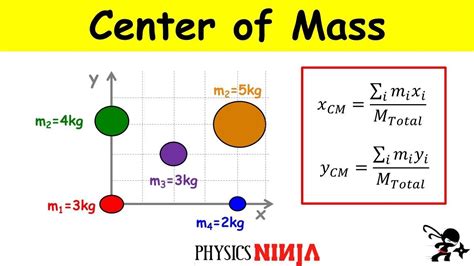
Before diving into semicircle center of mass, let's first understand what center of mass is. The center of mass is the point where the entire mass of an object can be considered to be concentrated. It's the point where the object would balance if it were placed on a fulcrum. The center of mass is a crucial concept in physics, as it helps us analyze and predict the motion of objects.
Importance of Center of Mass

Understanding the center of mass is essential in various fields, including engineering, physics, and architecture. It helps us:
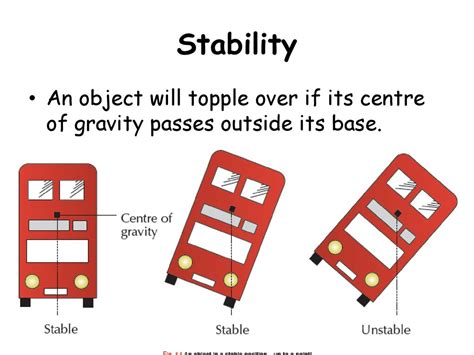
- Calculate the stability of objects
- Determine the motion of objects
- Design structures and buildings
- Analyze the behavior of complex systems
Semicircle Center of Mass: Definition and Calculation
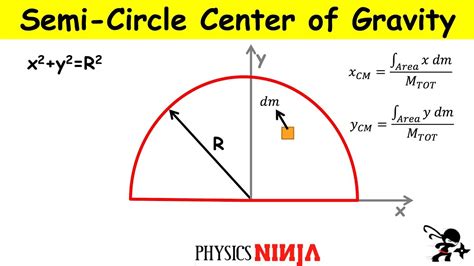
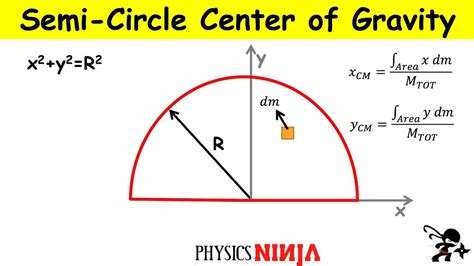
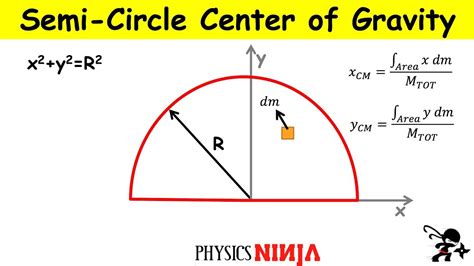
A semicircle is a two-dimensional shape that is half of a circle. To calculate the center of mass of a semicircle, we need to consider its geometry and mass distribution.
The center of mass of a semicircle can be calculated using the following formula:
x_cm = (4r)/(3π)
where x_cm is the x-coordinate of the center of mass, and r is the radius of the semicircle.
Derivation of the Formula
To derive the formula, we can use the definition of center of mass and the properties of a semicircle. The center of mass is the point where the entire mass of the semicircle can be considered to be concentrated. We can calculate the mass of the semicircle by integrating the area of the semicircle with respect to its radius.
Using the disk method, we can calculate the mass of the semicircle as:
m = ∫[0,r] (2πr) dm
where m is the mass of the semicircle, and dm is the mass of a small element of the semicircle.
Solving the integral, we get:
m = (πr^2)/2
Now, we can use the definition of center of mass to calculate the x-coordinate of the center of mass:
x_cm = ∫[0,r] x dm / ∫[0,r] dm
Substituting the expression for m, we get:
x_cm = (4r)/(3π)
Practical Applications of Semicircle Center of Mass
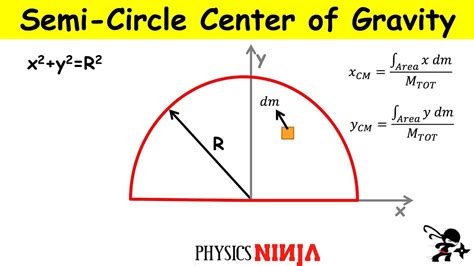
Understanding the center of mass of a semicircle has several practical applications:
- Designing curved structures: Knowing the center of mass of a semicircle helps architects and engineers design curved structures, such as bridges and arches.
- Analyzing the motion of objects: The center of mass of a semicircle is essential in understanding the motion of objects that have a curved shape.
- Calculating the stability of objects: The center of mass of a semicircle helps us calculate the stability of objects that have a curved base.
Gallery of Semicircle Center of Mass
Semicircle Center of Mass Image Gallery



Final Thoughts
In conclusion, the center of mass of a semicircle is a fundamental concept in physics and engineering. Understanding its definition, calculation methods, and practical applications can help us design and analyze curved structures, motion of objects, and stability of objects. We hope this article has provided you with a comprehensive understanding of semicircle center of mass. If you have any questions or comments, please feel free to share them below.
