Intro
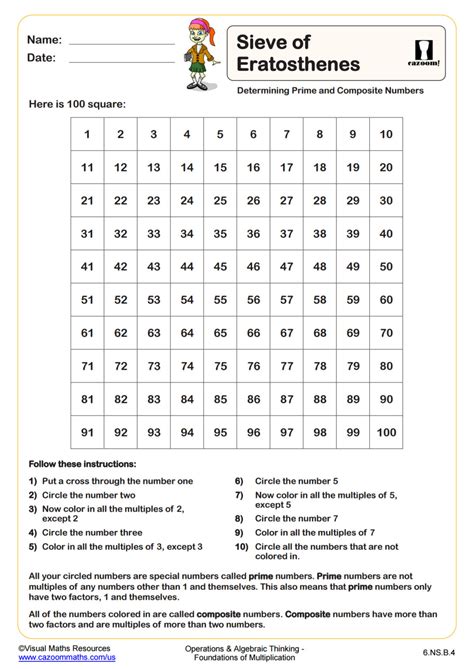
Unlock the secrets of prime numbers with the Sieve of Eratosthenes worksheet. Master this ancient algorithm in 5 easy steps and discover the efficient way to find all primes smaller than a given number. Boost your math skills and learn how to identify prime numbers quickly, improving your problem-solving abilities in number theory and mathematics.
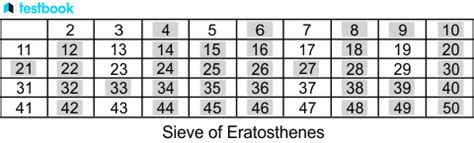
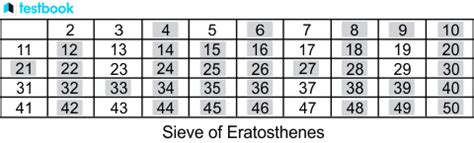
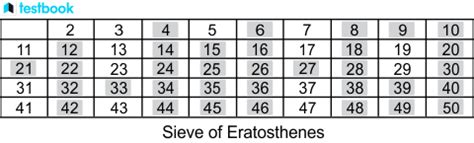
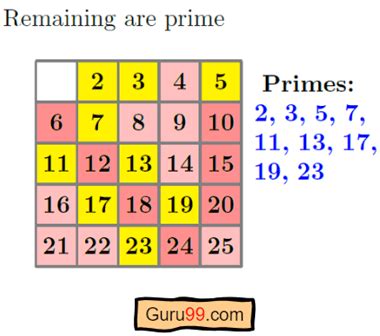
The Sieve of Eratosthenes is an ancient algorithm used to find all prime numbers up to a given number, called the limit. It's a fundamental concept in mathematics and computer science, and mastering it can be a valuable skill for anyone interested in coding, mathematics, or problem-solving. In this article, we'll explore five ways to master the Sieve of Eratosthenes worksheet, along with practical examples, explanations, and tips to help you improve your skills.

Understanding the Basics
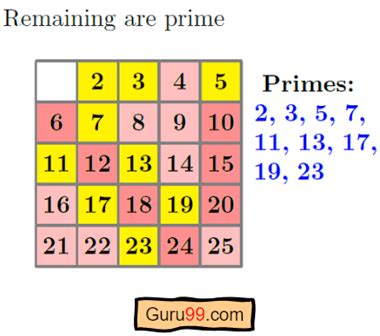
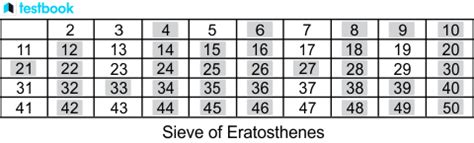
Before we dive into the advanced techniques, it's essential to understand the basic concept of the Sieve of Eratosthenes. The algorithm works by iteratively marking the multiples of each prime number starting from 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with a difference between them that is equal to that prime. This process is repeated until the square root of the limit is reached.
Step-by-Step Explanation
Here's a step-by-step explanation of the Sieve of Eratosthenes algorithm:
- Create a list of numbers from 2 to the limit.
- Start with the first prime number, 2.
- Mark all the multiples of 2, starting from 4.
- Move to the next unmarked number, which is 3.
- Mark all the multiples of 3, starting from 6.
- Repeat the process until the square root of the limit is reached.
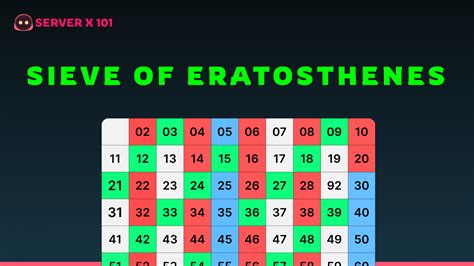
Method 1: Practice with Small Limits
One of the best ways to master the Sieve of Eratosthenes worksheet is to practice with small limits. Start with a limit of 10 or 20 and work your way up to larger limits. This will help you understand the pattern and the process of marking multiples.
Here's an example of the Sieve of Eratosthenes worksheet with a limit of 20:
| Number | Marked |
|---|---|
| 2 | |
| 3 | |
| 4 | X |
| 5 | |
| 6 | X |
| 7 | |
| 8 | X |
| 9 | X |
| 10 | X |
| 11 | |
| 12 | X |
| 13 | |
| 14 | X |
| 15 | X |
| 16 | X |
| 17 | |
| 18 | X |
| 19 | |
| 20 | X |
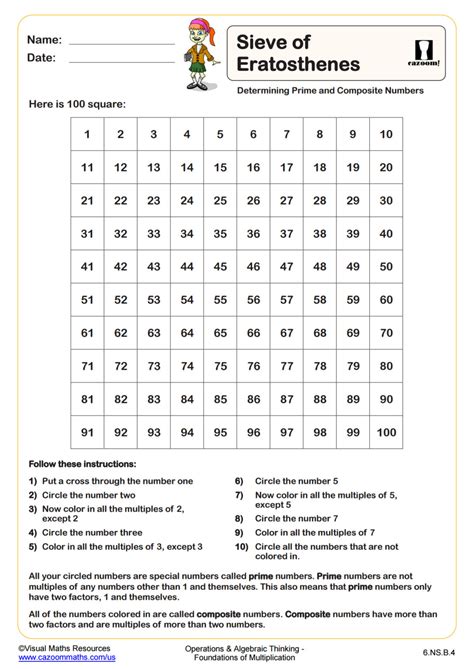
Method 2: Use a Table or Grid
Using a table or grid can help you visualize the Sieve of Eratosthenes worksheet and make it easier to mark multiples. You can create a table with columns for the numbers and rows for the prime numbers.
Here's an example of a table for the Sieve of Eratosthenes worksheet with a limit of 20:
| Prime | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 2 | X | | X | | X | | X | | X | | X | | X | | X | | X | | | 3 | | X | | X | | X | | X | | X | | X | | X | | X | | | 5 | | | | X | | X | | X | | X | | X | | X | |
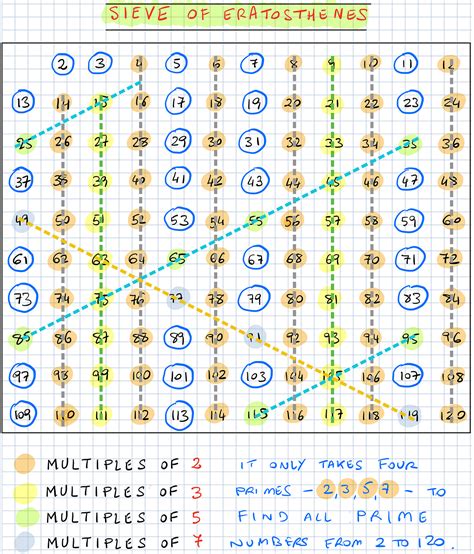
Method 3: Use a Computer Program
Using a computer program can help you master the Sieve of Eratosthenes worksheet by generating the multiples of prime numbers quickly and accurately. You can write a program in a programming language like Python or Java to generate the Sieve of Eratosthenes worksheet.
Here's an example of a Python program to generate the Sieve of Eratosthenes worksheet:
def sieve_of_eratosthenes(limit):
numbers = [True] * (limit + 1)
numbers[0] = numbers[1] = False
for i in range(2, int(limit ** 0.5) + 1):
if numbers[i]:
for j in range(i * i, limit + 1, i):
numbers[j] = False
return [p for p in range(2, limit + 1) if numbers[p]]
print(sieve_of_eratosthenes(20))
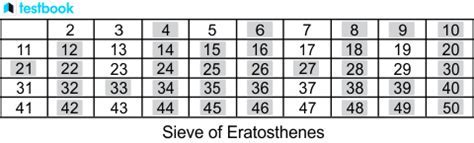
Method 4: Use a Calculator or Spreadsheet
Using a calculator or spreadsheet can help you master the Sieve of Eratosthenes worksheet by generating the multiples of prime numbers quickly and accurately. You can use a calculator like a graphing calculator or a spreadsheet like Google Sheets to generate the Sieve of Eratosthenes worksheet.
Here's an example of a Google Sheets formula to generate the Sieve of Eratosthenes worksheet:
=IF(A2>1,IF(MOD(A2,2)=0,"X",""), "")

Method 5: Practice with Different Types of Numbers
Finally, practicing with different types of numbers can help you master the Sieve of Eratosthenes worksheet. You can practice with odd numbers, even numbers, prime numbers, or composite numbers.
Here's an example of the Sieve of Eratosthenes worksheet with a limit of 20 and only odd numbers:
| Number | Marked |
|---|---|
| 3 | |
| 5 | |
| 7 | |
| 9 | X |
| 11 | |
| 13 | |
| 15 | X |
| 17 | |
| 19 |

Sieve of Eratosthenes Image Gallery


We hope this article has helped you master the Sieve of Eratosthenes worksheet. Remember to practice regularly and try different methods to improve your skills. If you have any questions or need further clarification, please leave a comment below. Don't forget to share this article with your friends and classmates who may benefit from it. Happy learning!
