5 Ways To Solve Matrix Equations In Excel

Matrix Equations in Excel: An Overview

Matrix equations are a fundamental concept in linear algebra and are used to solve systems of linear equations. In Excel, matrix equations can be used to solve a wide range of problems, from simple linear equations to complex systems of equations. However, solving matrix equations in Excel can be a bit tricky, especially for those who are new to linear algebra.

In this article, we will explore five ways to solve matrix equations in Excel. We will start with the basics of matrix equations and then move on to more advanced methods. By the end of this article, you will be able to solve matrix equations in Excel with ease.

What is a Matrix Equation?

A matrix equation is a mathematical expression that involves a matrix and one or more variables. The matrix is a rectangular array of numbers, and the variables are the unknowns that we want to solve for. Matrix equations can be represented in the following form:

AX = B

where A is the matrix, X is the variable matrix, and B is the constant matrix.

Types of Matrix Equations

There are several types of matrix equations, including:

• Linear matrix equations: These are the simplest type of matrix equation and involve a single matrix and a single variable.
• Nonlinear matrix equations: These involve multiple matrices and variables and are more complex to solve.
• Systems of matrix equations: These involve multiple matrix equations that need to be solved simultaneously.

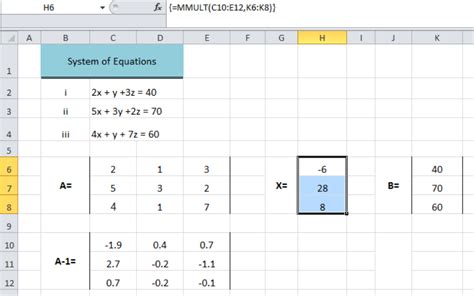
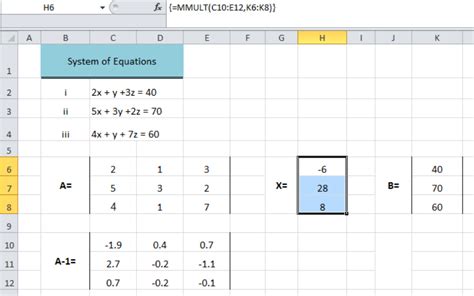
Method 1: Using the MMULT Function

The MMULT function is a built-in Excel function that can be used to solve matrix equations. The function takes two matrices as input and returns the product of the two matrices.

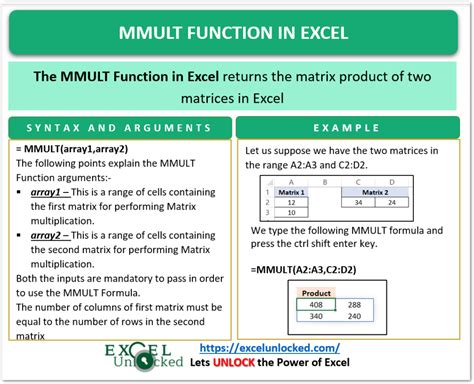
To use the MMULT function to solve a matrix equation, follow these steps:

1. Enter the matrix equation in the form AX = B.
2. Select the cell where you want to display the solution.
3. Type "=MMULT(A,B)" and press Enter.

For example, suppose we have the following matrix equation:

| 1 2 | | x | | 3 | | 3 4 | | y | | 5 |

To solve this equation using the MMULT function, we would enter the following formula:

=MMULT(A1:B2,C1:C2)

where A1:B2 is the matrix A and C1:C2 is the matrix B.

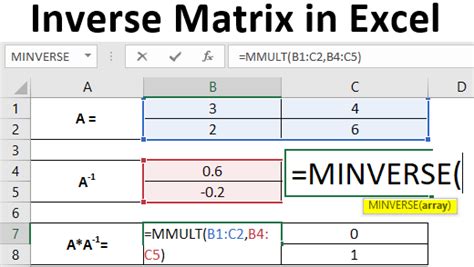
Method 2: Using the MINVERSE Function

The MINVERSE function is another built-in Excel function that can be used to solve matrix equations. The function takes a matrix as input and returns the inverse of the matrix.

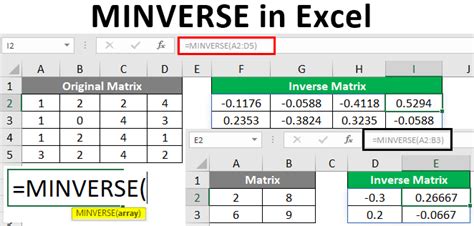
To use the MINVERSE function to solve a matrix equation, follow these steps:

1. Enter the matrix equation in the form AX = B.
2. Select the cell where you want to display the solution.
3. Type "=MINVERSE(A)" and press Enter.
4. Multiply the result by B.

For example, suppose we have the following matrix equation:

| 1 2 | | x | | 3 | | 3 4 | | y | | 5 |

To solve this equation using the MINVERSE function, we would enter the following formula:

=MINVERSE(A1:B2)*C1:C2

where A1:B2 is the matrix A and C1:C2 is the matrix B.

Method 3: Using Solver

Solver is an add-in in Excel that can be used to solve matrix equations. To use Solver, follow these steps:

1. Go to the Data tab and click on Solver.
2. Select the cell where you want to display the solution.
3. Click on "Set Target Cell" and select the cell that contains the equation.
4. Click on "By Changing Variable Cells" and select the cells that contain the variables.
5. Click on "Solve" to solve the equation.

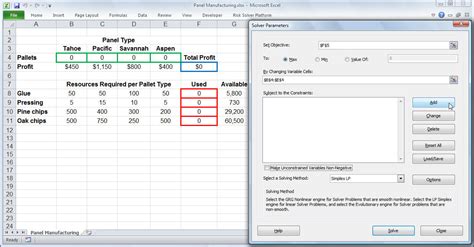
For example, suppose we have the following matrix equation:

| 1 2 | | x | | 3 | | 3 4 | | y | | 5 |

To solve this equation using Solver, we would select the cell that contains the equation, select the cells that contain the variables, and click on "Solve".

Method 4: Using VBA

VBA (Visual Basic for Applications) is a programming language that can be used to solve matrix equations in Excel. To use VBA, follow these steps:

1. Go to the Developer tab and click on Visual Basic.
2. Create a new module and paste the following code:

Sub SolveMatrixEquation() Dim A As Variant Dim B As Variant Dim X As Variant

' Define the matrix A
A = Range("A1:B2").Value

' Define the matrix B
B = Range("C1:C2").Value

' Solve the equation
X = Application.WorksheetFunction.MMult(Application.WorksheetFunction.MInverse(A), B)

' Display the solution
Range("E1:E2").Value = X

End Sub

3. Run the code by clicking on "Run" or by pressing F5.

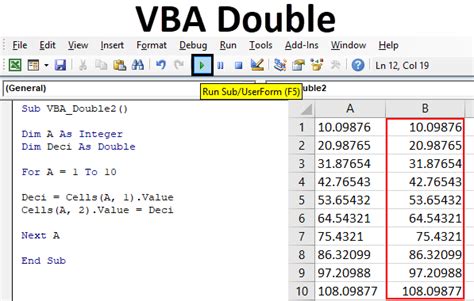
For example, suppose we have the following matrix equation:

| 1 2 | | x | | 3 | | 3 4 | | y | | 5 |

To solve this equation using VBA, we would paste the code into a new module and run it.

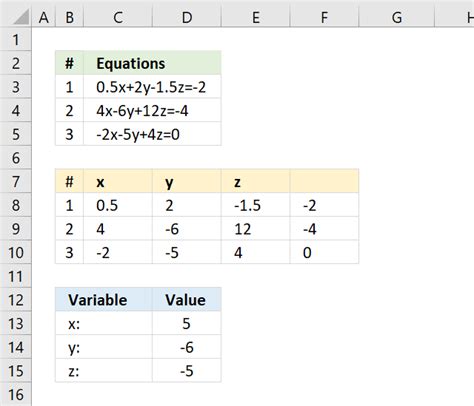
Method 5: Using a Matrix Inversion Formula

A matrix inversion formula is a mathematical formula that can be used to solve matrix equations. The formula is as follows:

X = A^(-1)B

where A is the matrix, X is the variable matrix, and B is the constant matrix.

To use the matrix inversion formula to solve a matrix equation, follow these steps:

1. Enter the matrix equation in the form AX = B.
2. Select the cell where you want to display the solution.
3. Type "=A^(-1)*B" and press Enter.

For example, suppose we have the following matrix equation:

| 1 2 | | x | | 3 | | 3 4 | | y | | 5 |

To solve this equation using the matrix inversion formula, we would enter the following formula:

=A1:B2^(-1)*C1:C2

where A1:B2 is the matrix A and C1:C2 is the matrix B.

Gallery of Matrix Equations in Excel

Matrix Equations in Excel Image Gallery

Conclusion

Matrix equations are a fundamental concept in linear algebra and are used to solve systems of linear equations. In Excel, matrix equations can be solved using a variety of methods, including the MMULT function, the MINVERSE function, Solver, VBA, and a matrix inversion formula. By using these methods, you can solve matrix equations in Excel with ease.

We hope this article has been helpful in explaining the different methods for solving matrix equations in Excel. If you have any questions or need further assistance, please don't hesitate to ask.