Intro
Discover how to easily calculate the Spearman Rank Correlation Coefficient in Excel. Learn the step-by-step process for measuring the strength and direction of a non-parametric relationship between two variables. Master non-linear correlations, statistical analysis, and data interpretation with this comprehensive guide, perfect for data analysis and statistical modeling in Excel.
In statistics, correlation is a measure of the relationship between two variables. One of the most widely used measures of correlation is the Spearman rank correlation coefficient, which assesses the strength and direction of the association between two ranked variables. In this article, we'll explore how to calculate the Spearman rank correlation coefficient in Excel, and provide examples to illustrate its application.
The Importance of Correlation Analysis
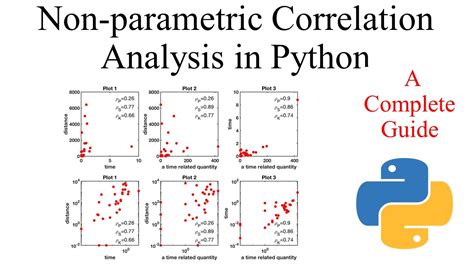
Correlation analysis is a crucial step in understanding the relationships between variables in a dataset. By analyzing the correlation between variables, researchers and analysts can identify patterns, trends, and relationships that can inform decision-making, prediction, and modeling. The Spearman rank correlation coefficient is particularly useful when dealing with ranked data, such as ordinal variables or non-normal continuous data.
What is the Spearman Rank Correlation Coefficient?
The Spearman rank correlation coefficient, denoted by ρ (rho), is a non-parametric measure of correlation that assesses the relationship between two ranked variables. It is calculated by ranking the data, calculating the difference between the ranks, and then applying a correlation formula. The resulting coefficient ranges from -1 to 1, where:
- ρ = 1 indicates a perfect positive correlation
- ρ = -1 indicates a perfect negative correlation
- ρ = 0 indicates no correlation
How to Calculate the Spearman Rank Correlation Coefficient in Excel
Excel provides a built-in function to calculate the Spearman rank correlation coefficient, which is the CORREL function. However, this function requires the data to be in a specific format, which can be time-consuming to prepare. Alternatively, you can use the following steps to calculate the Spearman rank correlation coefficient in Excel:
Step 1: Prepare the Data
Enter your data into two columns in Excel, ensuring that the data is in the same order.
Step 2: Rank the Data
Use the RANK function to rank the data in each column. For example, if your data is in columns A and B, you can use the following formulas:
- =RANK(A2,$A$2:$A$10)
- =RANK(B2,$B$2:$B$10)
Assuming your data is in cells A2:A10 and B2:B10.
Step 3: Calculate the Differences
Calculate the differences between the ranks using the following formula:
- =(A2-B2)^2
Assuming your ranked data is in cells A2 and B2.
Step 4: Calculate the Sum of the Squared Differences
Calculate the sum of the squared differences using the SUM function.
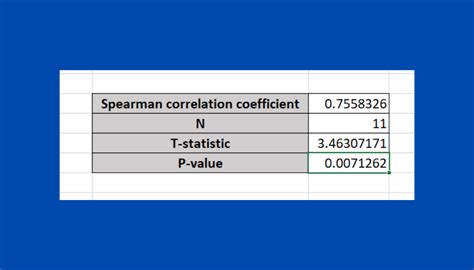
Step 5: Calculate the Spearman Rank Correlation Coefficient
Use the following formula to calculate the Spearman rank correlation coefficient:
- =1-(6*SUM(C2:C10))/(10*(10^2-1))
Assuming your data is in cells A2:A10 and B2:B10, and the sum of the squared differences is in cell C10.
Using the CORREL Function
Alternatively, you can use the CORREL function to calculate the Spearman rank correlation coefficient. This function requires the data to be in a specific format, which can be time-consuming to prepare.
Example
Suppose we have two variables, X and Y, with the following values:
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
| 4 | 4 |
| 5 | 5 |
To calculate the Spearman rank correlation coefficient, we can follow the steps outlined above.
Gallery of Spearman Rank Correlation Coefficient Images
Spearman Rank Correlation Coefficient Image Gallery
Conclusion and Next Steps
The Spearman rank correlation coefficient is a powerful tool for analyzing the relationship between two ranked variables. By following the steps outlined in this article, you can easily calculate the Spearman rank correlation coefficient in Excel. Whether you're a researcher, analyst, or student, mastering this technique will enhance your data analysis skills and help you make informed decisions.
We hope this article has provided valuable insights into the Spearman rank correlation coefficient and its application in Excel. If you have any questions or would like to share your experiences with correlation analysis, please leave a comment below.