5 Ways Spectral Clustering Math

Spectral clustering is a powerful technique used in machine learning and data analysis to group similar data points into clusters. It has gained popularity due to its ability to handle complex datasets and provide meaningful insights. In this article, we will delve into the world of spectral clustering math and explore five ways it can be applied to real-world problems.

The importance of spectral clustering lies in its ability to identify patterns and structures in data that may not be apparent through other clustering methods. By using spectral clustering, researchers and data analysts can uncover hidden relationships between data points and gain a deeper understanding of the underlying mechanisms that drive complex systems. Whether it's analyzing customer behavior, identifying gene expression patterns, or segmenting images, spectral clustering has become an essential tool in the data scientist's toolkit.

Spectral clustering math is based on the idea of representing a dataset as a graph, where each data point is a node, and the edges between nodes represent the similarity between the data points. The graph is then transformed into a matrix, known as the adjacency matrix, which is used to compute the eigenvectors and eigenvalues. These eigenvectors and eigenvalues are used to cluster the data points into groups. The math behind spectral clustering is complex, but the results are well worth the effort.

Introduction to Spectral Clustering

Spectral clustering is a type of clustering algorithm that uses the eigenvalues and eigenvectors of a matrix to cluster data points. The algorithm works by first constructing a similarity matrix, which represents the similarity between each pair of data points. The similarity matrix is then used to compute the eigenvalues and eigenvectors, which are used to cluster the data points.

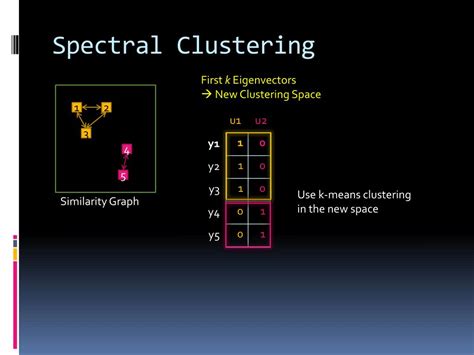
Key Components of Spectral Clustering

The key components of spectral clustering are: * Similarity matrix: This is a matrix that represents the similarity between each pair of data points. * Eigenvalues and eigenvectors: These are computed from the similarity matrix and are used to cluster the data points. * Clustering algorithm: This is the algorithm used to cluster the data points based on the eigenvalues and eigenvectors.

5 Ways Spectral Clustering Math Works

Spectral clustering math works in the following five ways: 1. **Data Representation**: Spectral clustering represents the data as a graph, where each data point is a node, and the edges between nodes represent the similarity between the data points. 2. **Similarity Matrix**: The algorithm constructs a similarity matrix, which represents the similarity between each pair of data points. 3. **Eigenvalue Decomposition**: The similarity matrix is then used to compute the eigenvalues and eigenvectors, which are used to cluster the data points. 4. **Clustering Algorithm**: The clustering algorithm is used to cluster the data points based on the eigenvalues and eigenvectors. 5. **Evaluation Metrics**: The quality of the clustering is evaluated using metrics such as silhouette score, calinski-harabasz index, and davies-bouldin index.

Advantages of Spectral Clustering

The advantages of spectral clustering are: * **Handling Non-Linear Relationships**: Spectral clustering can handle non-linear relationships between data points. * **Robustness to Noise**: Spectral clustering is robust to noise and outliers in the data. * **Flexibility**: Spectral clustering can be used with a variety of clustering algorithms.

Applications of Spectral Clustering

Spectral clustering has a wide range of applications in: * **Image Segmentation**: Spectral clustering is used in image segmentation to segment images into regions of similar texture and color. * **Gene Expression Analysis**: Spectral clustering is used in gene expression analysis to identify patterns of gene expression. * **Customer Segmentation**: Spectral clustering is used in customer segmentation to segment customers based on their behavior and demographics.

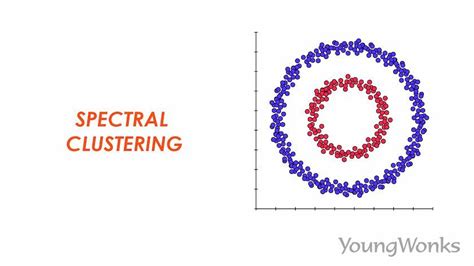
Real-World Examples of Spectral Clustering

Some real-world examples of spectral clustering are: * **Image Segmentation**: Spectral clustering is used in image segmentation to segment images of tumors into regions of similar texture and color. * **Gene Expression Analysis**: Spectral clustering is used in gene expression analysis to identify patterns of gene expression in cancer cells. * **Customer Segmentation**: Spectral clustering is used in customer segmentation to segment customers based on their behavior and demographics.

Challenges and Limitations of Spectral Clustering

Spectral clustering has several challenges and limitations, including: * **Computational Complexity**: Spectral clustering can be computationally expensive, especially for large datasets. * **Choice of Parameters**: The choice of parameters, such as the number of clusters, can be challenging. * **Interpretability**: The results of spectral clustering can be difficult to interpret.

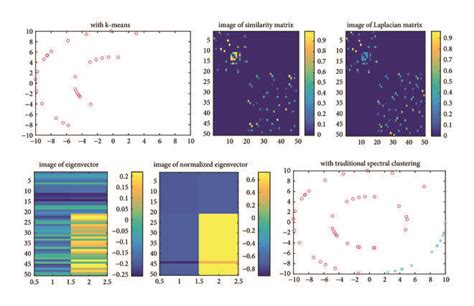
Future Directions of Spectral Clustering

The future directions of spectral clustering include: * **Development of New Algorithms**: The development of new algorithms that can handle large datasets and non-linear relationships. * **Application to New Domains**: The application of spectral clustering to new domains, such as social network analysis and recommender systems. * **Integration with Other Techniques**: The integration of spectral clustering with other techniques, such as deep learning and natural language processing.

Gallery of Spectral Clustering Images

Spectral Clustering Image Gallery

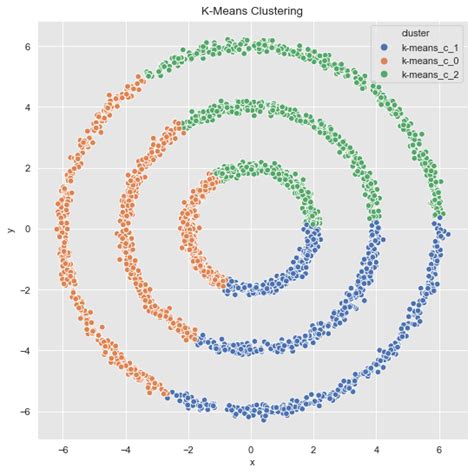
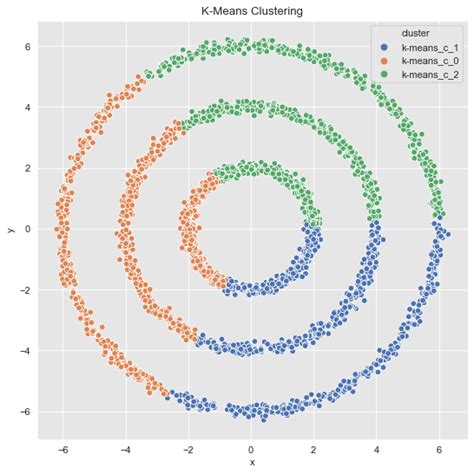
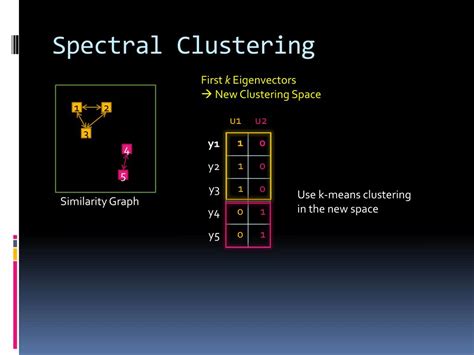
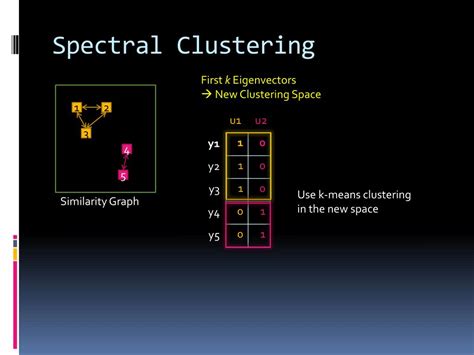
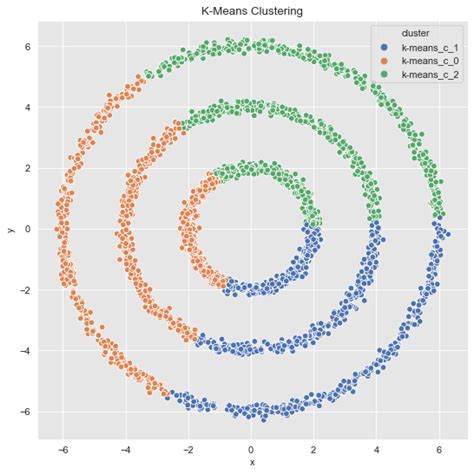
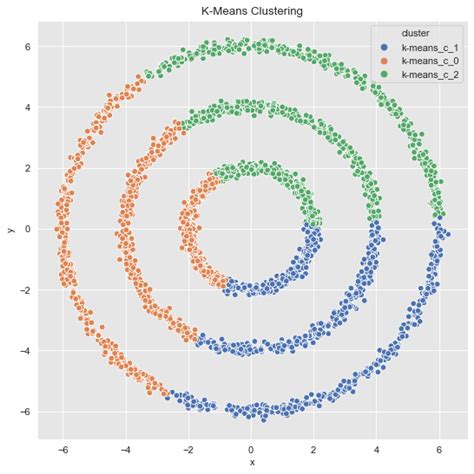
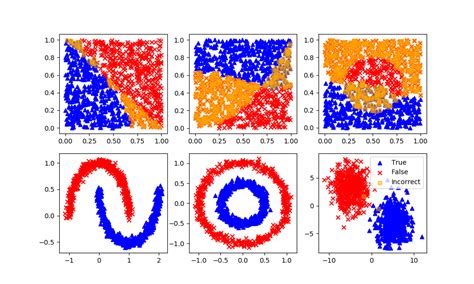
We hope this article has provided you with a comprehensive understanding of spectral clustering math and its applications. Whether you're a researcher, data analyst, or simply interested in machine learning, spectral clustering is a powerful technique that can help you uncover hidden patterns and relationships in complex datasets. We invite you to share your thoughts and experiences with spectral clustering in the comments below, and don't forget to share this article with your colleagues and friends who may be interested in this topic.