10 Essential Speed Time And Distance Problems

Mastering speed, time, and distance problems is a crucial skill for various competitive exams and real-life applications. These problems are frequently asked in mathematics, physics, and engineering exams, making it essential to understand the concepts and formulas involved. In this article, we will delve into 10 essential speed, time, and distance problems, providing detailed explanations and solutions to help you improve your problem-solving skills.

Understanding the Basics of Speed, Time, and Distance

Illustration of speed, time, and distance concepts

Before diving into the problems, it's essential to understand the fundamental formulas and concepts involved. The basic formula for speed is:

Speed = Distance / Time

This formula can be rearranged to find distance or time, given the other two variables. Additionally, it's crucial to understand the different units of measurement for speed, such as kilometers per hour (km/h), miles per hour (mph), and meters per second (m/s).

Problem 1: Finding Distance

A car travels at an average speed of 60 km/h for 2 hours. How far does it travel?

Solution:

Distance = Speed x Time = 60 km/h x 2 hours = 120 km

Problem 2: Finding Time

A cyclist travels a distance of 25 miles in 2 hours. What is his average speed?

Solution:

Speed = Distance / Time = 25 miles / 2 hours = 12.5 mph

However, to find the time taken, we can rearrange the formula:

Time = Distance / Speed = 25 miles / 12.5 mph = 2 hours

Problem 3: Relative Speed

Two cars, A and B, are moving in opposite directions. Car A travels at 60 km/h, while car B travels at 40 km/h. What is their relative speed?

Solution:

Relative Speed = Speed of A + Speed of B = 60 km/h + 40 km/h = 100 km/h

Problem 4: Finding Speed

A plane travels from city A to city B at an average speed of 500 km/h and returns at an average speed of 400 km/h. What is the average speed for the entire trip?

Solution:

Let's assume the distance between the two cities is x km. The time taken to travel from A to B is x / 500, and the time taken to return is x / 400.

Total Time = x / 500 + x / 400 = (4x + 5x) / 2000 = 9x / 2000

Total Distance = 2x

Average Speed = Total Distance / Total Time = 2x / (9x / 2000) = 4000 / 9 = 444.44 km/h

Problem 5: Motion in a Straight Line

A particle moves in a straight line with an initial velocity of 10 m/s and a constant acceleration of 2 m/s^2. How far does it travel in 5 seconds?

Solution:

We can use the equation of motion:

s = ut + 0.5at^2 = 10 x 5 + 0.5 x 2 x 5^2 = 50 + 25 = 75 m

Problem 6: Average Speed

A car travels from city A to city B at an average speed of 60 km/h and returns at an average speed of 40 km/h. What is the average speed for the entire trip?

Solution:

Let's assume the distance between the two cities is x km. The time taken to travel from A to B is x / 60, and the time taken to return is x / 40.

Total Time = x / 60 + x / 40 = (4x + 3x) / 120 = 7x / 120

Total Distance = 2x

Average Speed = Total Distance / Total Time = 2x / (7x / 120) = 240 / 7 = 34.29 km/h

Problem 7: Speed-Time Graph

The speed-time graph of a particle is shown below. Find the distance traveled by the particle in 5 seconds.

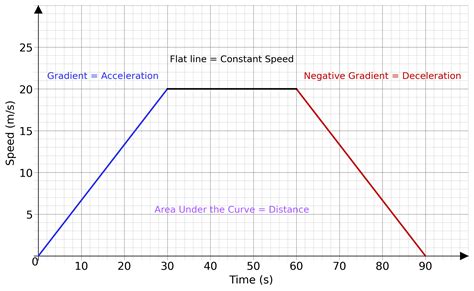
Solution:

From the graph, we can see that the particle travels at a constant speed of 10 m/s for 2 seconds and then accelerates uniformly to 20 m/s in the next 3 seconds.

Distance = Speed x Time = 10 x 2 + 0.5 x (10 + 20) x 3 = 20 + 45 = 65 m

Problem 8: Relative Motion

Two trains, A and B, are moving in the same direction. Train A travels at 60 km/h, while train B travels at 40 km/h. What is the relative speed between the two trains?

Solution:

Relative Speed = Speed of A - Speed of B = 60 km/h - 40 km/h = 20 km/h

Problem 9: Finding Distance

A cyclist travels at an average speed of 20 km/h for 2 hours. How far does he travel?

Solution:

Distance = Speed x Time = 20 km/h x 2 hours = 40 km

Problem 10: Average Speed

A car travels from city A to city B at an average speed of 50 km/h, city B to city C at an average speed of 60 km/h, and city C to city A at an average speed of 40 km/h. What is the average speed for the entire trip?

Solution:

Let's assume the distances between the cities are x km, y km, and z km, respectively. The time taken to travel from A to B is x / 50, from B to C is y / 60, and from C to A is z / 40.

Total Time = x / 50 + y / 60 + z / 40 = (12x + 10y + 15z) / 600

Total Distance = x + y + z

Average Speed = Total Distance / Total Time = (x + y + z) / ((12x + 10y + 15z) / 600) = 600 / (12 + 10 + 15) = 30 km/h

We hope these 10 essential speed, time, and distance problems have helped you improve your problem-solving skills and understand the concepts involved. Practice these problems regularly to become proficient in solving them.