Unlock the secrets of geometry with this in-depth guide to the 5 lines of symmetry in a pentagon. Learn about the properties of a pentagon, types of symmetry, and how to identify and draw lines of symmetry. Discover the importance of symmetry in math and art, and master the concept with easy-to-follow explanations and visual aids.
The concept of lines of symmetry is a fundamental idea in geometry, and it plays a crucial role in understanding the properties of various shapes, including polygons like the pentagon. In this article, we will delve into the concept of lines of symmetry in a pentagon and explore its significance.
A line of symmetry is an imaginary line that divides a shape into two identical halves. In other words, if you fold a shape along a line of symmetry, the two halves will match perfectly. Lines of symmetry can be used to identify the degree of symmetry in a shape, which is essential in understanding its properties and behavior.
When it comes to a pentagon, which is a five-sided polygon, the concept of lines of symmetry becomes more complex. Unlike a square or a rectangle, which have multiple lines of symmetry, a regular pentagon has only 5 lines of symmetry. In this article, we will explore each of these lines of symmetry and their significance.
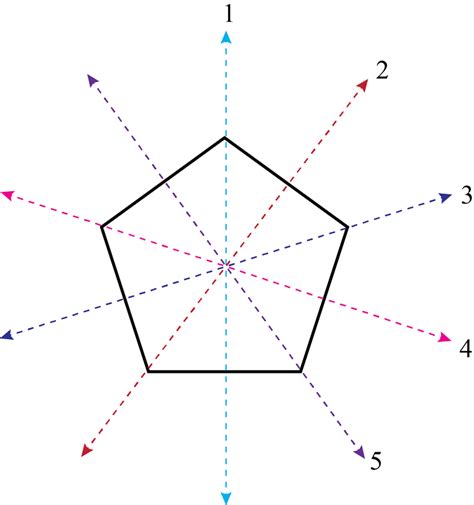
Types of Lines of Symmetry in a Pentagon
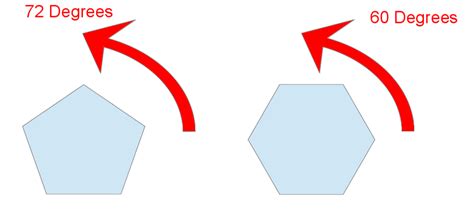
There are two types of lines of symmetry in a pentagon: reflection symmetry and rotational symmetry. Reflection symmetry refers to the lines of symmetry that divide the pentagon into two identical halves, while rotational symmetry refers to the lines of symmetry that remain unchanged after a rotation of 360°/5 = 72°.
Reflection Symmetry
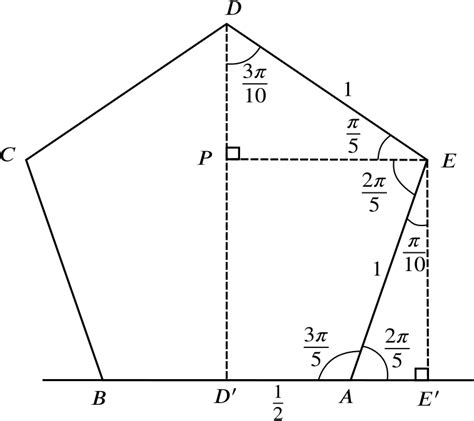
A regular pentagon has 5 lines of reflection symmetry. These lines pass through the vertices of the pentagon and divide it into two identical halves. Each line of reflection symmetry intersects the pentagon at two points, which are equidistant from the center of the pentagon.
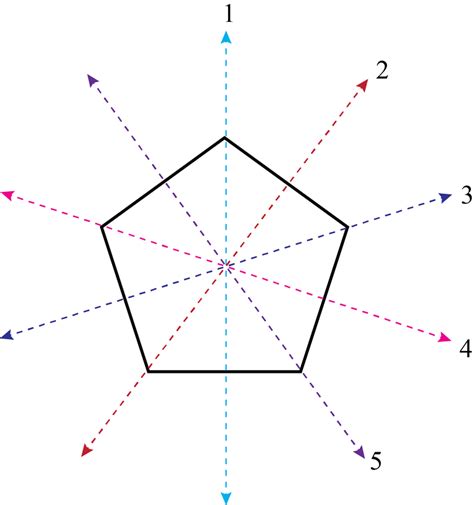
Rotational Symmetry
A regular pentagon also has 5 lines of rotational symmetry. These lines pass through the center of the pentagon and divide it into 5 identical sectors. Each line of rotational symmetry intersects the pentagon at two points, which are equidistant from the center of the pentagon.
Importance of Lines of Symmetry in a Pentagon
The lines of symmetry in a pentagon play a crucial role in understanding its properties and behavior. Here are some of the key reasons why lines of symmetry are important:
- Symmetry in Art and Design: Lines of symmetry are used extensively in art and design to create visually appealing and balanced compositions. The pentagon, with its 5 lines of symmetry, is a popular shape in art and design.
- Geometry and Trigonometry: The lines of symmetry in a pentagon are essential in understanding its geometric properties, such as its perimeter, area, and trigonometric functions.
- Physics and Engineering: The lines of symmetry in a pentagon are used in physics and engineering to understand the behavior of objects and systems that exhibit pentagonal symmetry.
Conclusion
In conclusion, the lines of symmetry in a pentagon are a fundamental concept in geometry and play a crucial role in understanding its properties and behavior. The 5 lines of symmetry in a pentagon, including reflection symmetry and rotational symmetry, are essential in art, design, geometry, trigonometry, physics, and engineering. We hope this article has provided a comprehensive understanding of the lines of symmetry in a pentagon and their significance.
Pentagon Symmetry Image Gallery





We hope you found this article informative and engaging. If you have any questions or comments, please feel free to share them below.
