Discover the surprising truth about penny terminal velocity! Learn how fast a penny can fall, the science behind its terminal velocity, and the factors that affect its descent. Explore the physics of free fall, air resistance, and terminal velocity, and find out what happens when a penny reaches its maximum falling speed.
When it comes to objects falling towards the ground, our curiosity often gets the better of us. We've all dropped something at some point, watching in slow motion as it plummets towards the earth. But have you ever stopped to think about the terminal velocity of a penny? How fast can it fall before air resistance kicks in and slows it down?
The concept of terminal velocity is an intriguing one, and it's not just limited to pennies. Any object that falls through the air will eventually reach a point where the force of gravity is balanced by the force of air resistance, causing it to fall at a constant speed. But what's the terminal velocity of a penny, and how does it compare to other objects?

What is Terminal Velocity?
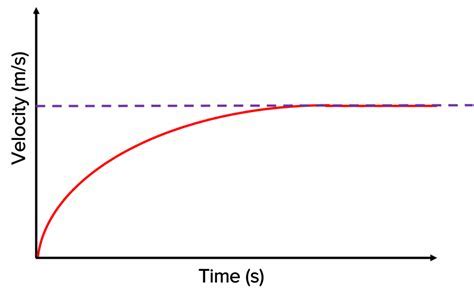
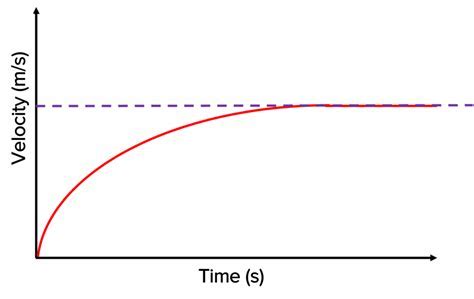
Before we dive into the terminal velocity of a penny, it's essential to understand the concept of terminal velocity itself. Terminal velocity is the maximum speed an object can reach as it falls through a fluid, such as air or water. At this point, the force of gravity pulling the object down is balanced by the force of friction, or air resistance, pushing the object up.
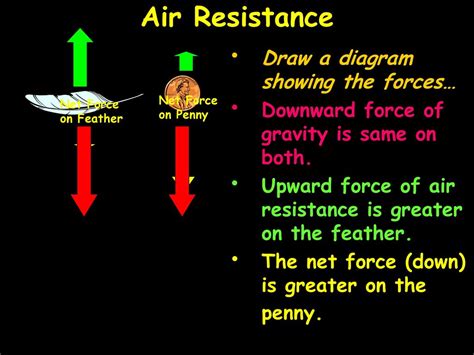
The terminal velocity of an object depends on several factors, including its mass, shape, and size, as well as the density of the fluid it's falling through. For example, a feather and a penny have different terminal velocities because of their different shapes and sizes.
Calculating Terminal Velocity
To calculate the terminal velocity of an object, we can use the following formula:
v = √(2mg/CdρA)
Where:
- v is the terminal velocity
- m is the mass of the object
- g is the acceleration due to gravity (approximately 9.8 m/s² on earth)
- Cd is the drag coefficient, which depends on the shape of the object
- ρ is the density of the fluid (air, in this case)
- A is the cross-sectional area of the object
The Terminal Velocity of a Penny
So, what's the terminal velocity of a penny? To calculate it, we need to know the mass, shape, and size of a penny. A standard US penny weighs 2.5 grams and has a diameter of 0.75 inches (1.9 cm).
Using the formula above, we can estimate the terminal velocity of a penny to be around 35-50 mph (56-80 km/h). However, this is just an estimate, and the actual terminal velocity of a penny may be different due to various factors, such as air turbulence and the penny's orientation during flight.
Comparing Terminal Velocities
To put the terminal velocity of a penny into perspective, let's compare it to other objects. For example:
- A skydiver can reach terminal velocities of up to 120 mph (193 km/h)
- A baseball can reach terminal velocities of up to 95 mph (153 km/h)
- A feather can reach terminal velocities of up to 5 mph (8 km/h)
As you can see, the terminal velocity of a penny is relatively low compared to other objects. This is because pennies are small and dense, with a low cross-sectional area, which reduces air resistance.
Factors Affecting Terminal Velocity
While the terminal velocity of a penny may seem like a fixed value, there are several factors that can affect it. For example:
- Air density: Changes in air density can affect the terminal velocity of an object. For example, a penny falling through thin air at high altitudes may reach a higher terminal velocity than one falling through dense air at sea level.
- Air turbulence: Turbulent air can disrupt the airflow around an object, affecting its terminal velocity. For example, a penny falling through a windy or stormy area may experience more air resistance than one falling through calm air.
- Object orientation: The orientation of an object during flight can affect its terminal velocity. For example, a penny falling flat-side down may experience more air resistance than one falling edge-on.

Practical Applications
Understanding the terminal velocity of a penny may seem like a trivial pursuit, but it has practical applications in various fields, such as:
- Aerodynamics: Studying the terminal velocity of objects can help us understand the principles of aerodynamics and improve our designs for aircraft, spacecraft, and other vehicles.
- Engineering: Knowing the terminal velocity of an object can help engineers design safer and more efficient systems, such as parachutes and airbags.
- Science: Researching the terminal velocity of objects can help us better understand the fundamental laws of physics and improve our understanding of the natural world.
Conclusion
In conclusion, the terminal velocity of a penny is a fascinating topic that reveals the complex interactions between objects and the air around them. By understanding the factors that affect terminal velocity, we can gain insights into the fundamental laws of physics and improve our designs for various applications.
Whether you're a scientist, engineer, or simply a curious observer, the terminal velocity of a penny is a fascinating topic that's worth exploring further.
Penny Terminal Velocity Image Gallery





We hope you've enjoyed this in-depth exploration of the terminal velocity of a penny. Whether you're a science enthusiast or simply a curious observer, we encourage you to share your thoughts and questions in the comments below.
