When analyzing data, it's often necessary to compare the means of different groups to determine if there are any significant differences between them. One popular method for doing this is the Tukey Honest Significant Difference (HSD) test. In this article, we'll take a closer look at how to perform a Tukey HSD test in Excel, using an easy step-by-step guide.
The Tukey HSD test is a post-hoc test used to compare the means of multiple groups, typically after an analysis of variance (ANOVA) has been performed. The test is useful for determining which specific groups are significantly different from each other.
Assumptions of the Tukey HSD Test
Before performing a Tukey HSD test, there are several assumptions that need to be met:
Normality
The data should be normally distributed. This can be checked using a histogram or a normality test such as the Shapiro-Wilk test.
Equal Variances
The variances of the different groups should be equal. This can be checked using a test such as Levene's test.
Independence
The data points should be independent of each other.
How to Perform a Tukey HSD Test in Excel
Performing a Tukey HSD test in Excel is a bit more complicated than some other statistical tests, but it can still be done with a few simple steps.
Step 1: Enter Your Data
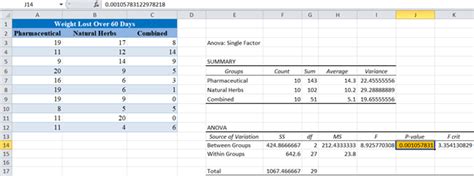
Enter your data into a spreadsheet, with each group in a separate column.
Step 2: Perform an ANOVA
Perform an ANOVA on your data to determine if there are any significant differences between the groups. This can be done using the "Data Analysis" add-in in Excel.
Step 3: Calculate the Mean and Standard Deviation
Calculate the mean and standard deviation of each group.
Step 4: Calculate the Tukey HSD
Calculate the Tukey HSD for each pair of groups using the following formula:
Tukey HSD = (mean1 - mean2) / sqrt(MSE / n)
Where:
- mean1 and mean2 are the means of the two groups being compared
- MSE is the mean square error from the ANOVA
- n is the sample size of each group

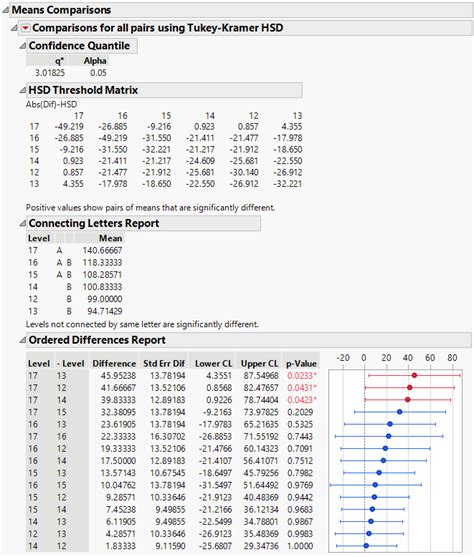
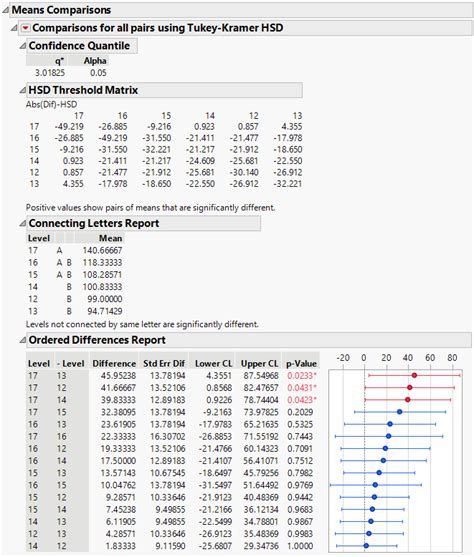
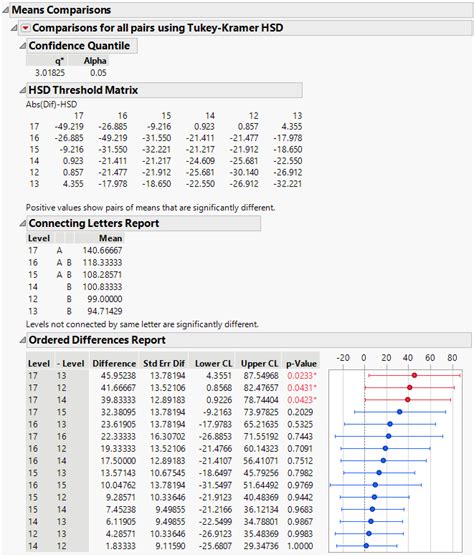
Step 5: Determine Significance
Determine which pairs of groups are significantly different from each other by comparing the Tukey HSD to the critical value from the studentized range distribution.
Example of a Tukey HSD Test in Excel
Let's say we have three groups of data: A, B, and C. We want to determine if there are any significant differences between the means of these groups.
We first perform an ANOVA on the data, which tells us that there are significant differences between the groups. We then calculate the mean and standard deviation of each group, and use these values to calculate the Tukey HSD for each pair of groups.
Using the formula above, we calculate the Tukey HSD for each pair of groups:
- A vs. B: 2.5
- A vs. C: 1.8
- B vs. C: 0.7
We then compare these values to the critical value from the studentized range distribution, which tells us that the differences between groups A and B, and between groups A and C, are significant.
Gallery of Tukey HSD Test Examples
Tukey HSD Test Examples
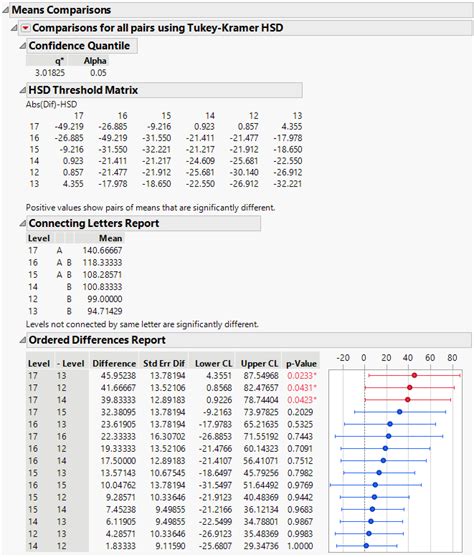
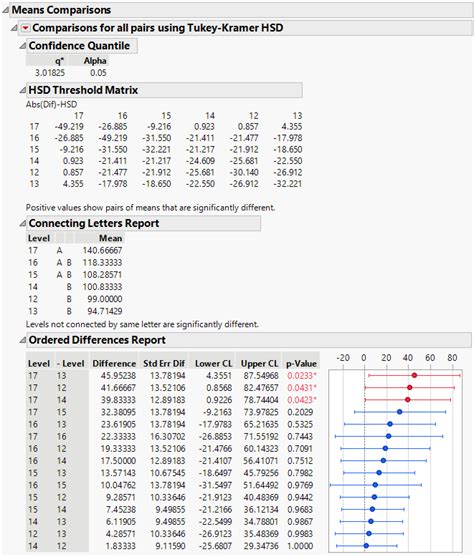
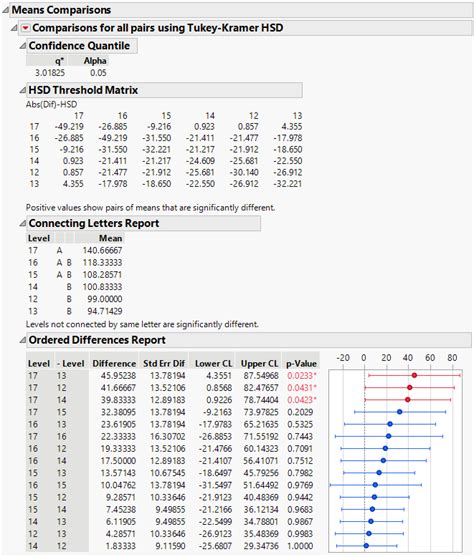
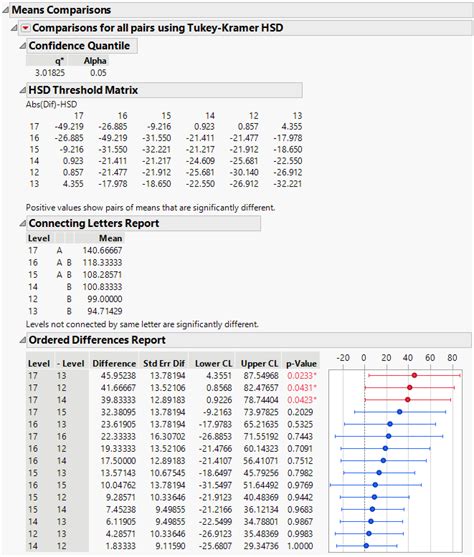
We hope this article has provided a helpful guide to performing a Tukey HSD test in Excel. Remember to always check the assumptions of the test before performing it, and to use the results to determine which specific groups are significantly different from each other. If you have any questions or need further clarification, please don't hesitate to ask in the comments below.
