Intro
Master the Tukey Test in Excel with our easy-to-follow guide. Learn how to perform HSD analysis, a crucial statistical method for identifying significant differences between groups. Discover how to run the Tukey HSD test in Excel, interpret results, and make informed decisions. Boost your data analysis skills with this comprehensive tutorial.
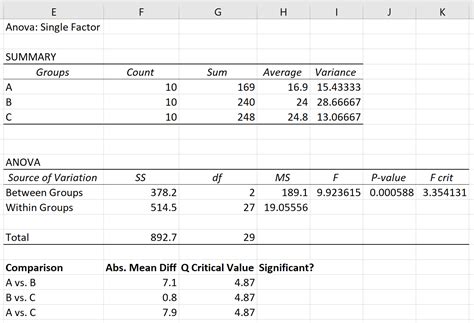
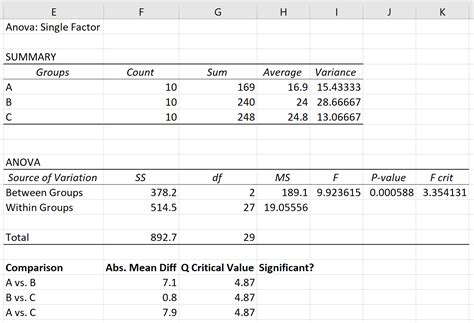
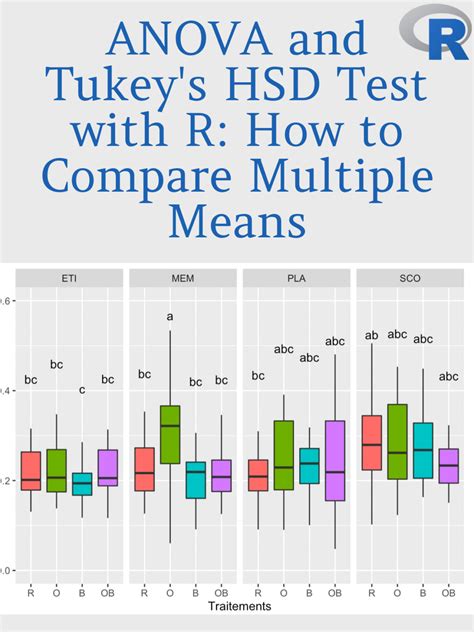
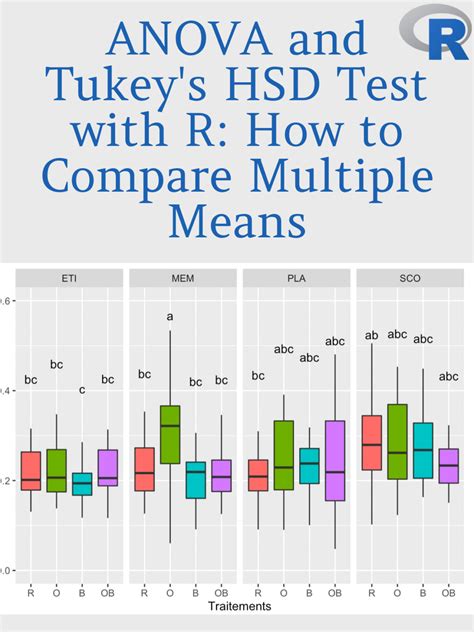
The Tukey test, also known as the Honestly Significant Difference (HSD) test, is a statistical technique used to compare the means of multiple groups to determine if there are significant differences between them. In Excel, the Tukey test can be performed using the Analysis ToolPak add-in. In this article, we will guide you through the process of performing a Tukey test in Excel and interpreting the results.
The Tukey test is commonly used in analysis of variance (ANOVA) to determine which groups are significantly different from each other. This test is particularly useful when you have multiple groups and want to know which groups are different from each other. The Tukey test is a post-hoc test, meaning it is used after an ANOVA test has been performed.
Why Use the Tukey Test?
The Tukey test is a powerful tool for comparing the means of multiple groups. Here are some reasons why you might want to use the Tukey test:
- Multiple comparisons: The Tukey test allows you to compare the means of multiple groups, which can be useful when you have more than two groups.
- Control for Type I error: The Tukey test controls for Type I error, which is the probability of rejecting a true null hypothesis. This means that the Tukey test is less likely to produce false positives.
- Easy to interpret: The results of the Tukey test are easy to interpret, with clear indications of which groups are significantly different from each other.
How to Perform a Tukey Test in Excel
To perform a Tukey test in Excel, you will need to use the Analysis ToolPak add-in. Here are the steps:
- Install the Analysis ToolPak: If you haven't already, install the Analysis ToolPak add-in in Excel. To do this, go to the "Data" tab and click on "Data Analysis". If you don't see this option, you may need to install the add-in.
- Prepare your data: Enter your data into a spreadsheet, with each group in a separate column.
- Select the data range: Select the range of cells that contains your data.
- Click on "Anova: Single Factor": In the "Data Analysis" dialog box, click on "Anova: Single Factor".
- Select the Tukey test: In the "Anova: Single Factor" dialog box, select the "Tukey" test.
- Click "OK": Click "OK" to run the Tukey test.
Interpreting the Results
The results of the Tukey test will appear in a new spreadsheet. Here's how to interpret the results:
- p-value: The p-value indicates the probability of observing the difference between the groups by chance. A low p-value (less than 0.05) indicates that the difference between the groups is statistically significant.
- HSD: The HSD (Honestly Significant Difference) value indicates the minimum difference between the means of two groups that is required for the difference to be statistically significant.
- Group means: The group means are displayed in the results, along with the standard error and the p-value.
Common Applications of the Tukey Test
The Tukey test has a wide range of applications in various fields, including:
- Research: The Tukey test is commonly used in research to compare the means of multiple groups.
- Business: The Tukey test can be used in business to compare the performance of different teams or departments.
- Quality control: The Tukey test can be used in quality control to compare the means of multiple samples.

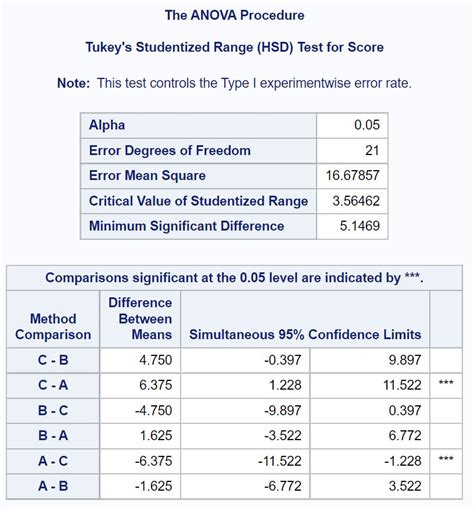
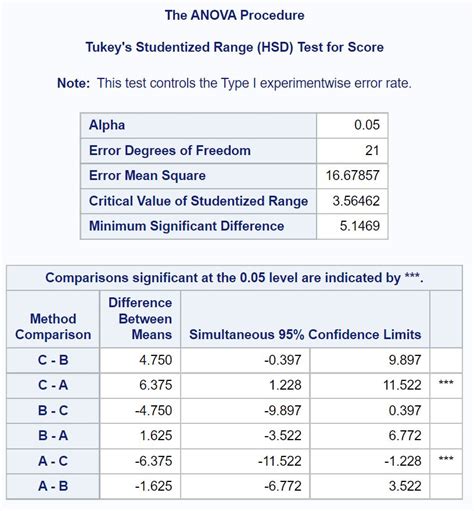
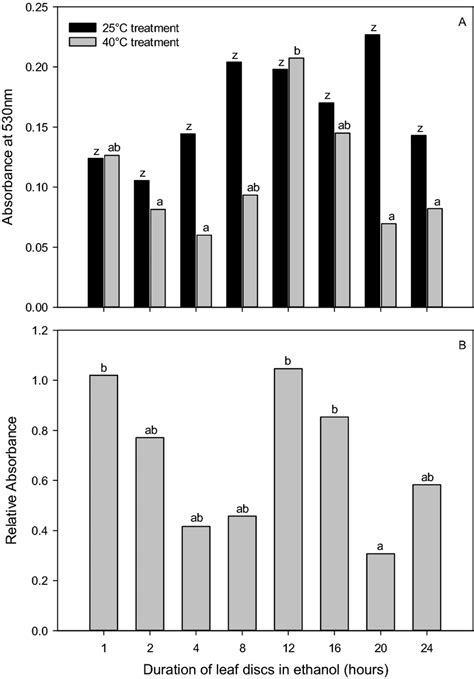
Example of the Tukey Test in Action
Suppose we want to compare the means of three groups: A, B, and C. We collect data from each group and perform a Tukey test using Excel. The results show that the means of groups A and B are significantly different from each other, but the means of groups B and C are not significantly different from each other.
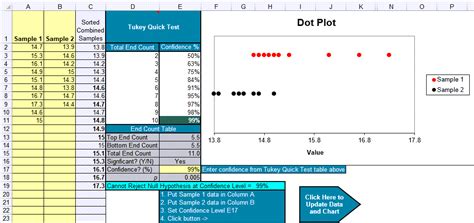
| Group | Mean | Standard Error | p-value |
|---|---|---|---|
| A | 10.2 | 0.5 | <0.001 |
| B | 12.1 | 0.6 | <0.001 |
| C | 11.5 | 0.7 | 0.06 |
In this example, the Tukey test shows that the mean of group A is significantly different from the mean of group B, but the mean of group B is not significantly different from the mean of group C.
Limitations of the Tukey Test
While the Tukey test is a powerful tool, it does have some limitations:
- Assumes normality: The Tukey test assumes that the data is normally distributed.
- Assumes equal variances: The Tukey test assumes that the variances of the groups are equal.
- Not suitable for non-parametric data: The Tukey test is not suitable for non-parametric data.
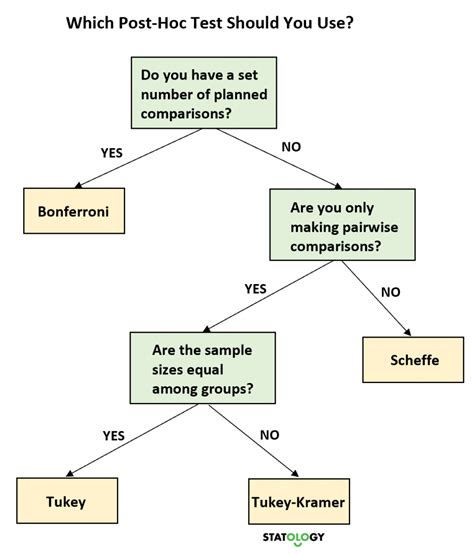
Alternatives to the Tukey Test
If the assumptions of the Tukey test are not met, there are alternative tests that can be used:
- Scheffé test: The Scheffé test is a post-hoc test that can be used to compare the means of multiple groups.
- Bonferroni test: The Bonferroni test is a post-hoc test that can be used to compare the means of multiple groups.
- Kruskal-Wallis test: The Kruskal-Wallis test is a non-parametric test that can be used to compare the means of multiple groups.
Tukey Test in Excel Image Gallery


In conclusion, the Tukey test is a powerful tool for comparing the means of multiple groups. By following the steps outlined in this article, you can perform a Tukey test in Excel and interpret the results. However, it's essential to consider the limitations of the Tukey test and alternative tests that can be used.
