Intro
Unlock the secrets to mastering UCL and LCL formulas with our expert guide. Learn 5 essential methods to accurately calculate Upper and Lower Control Limits, ensuring precision in statistical process control. Discover how to apply these formulas to enhance quality control, reduce variability, and improve manufacturing processes, using key statistics concepts like mean, standard deviation, and subgroup sizes.
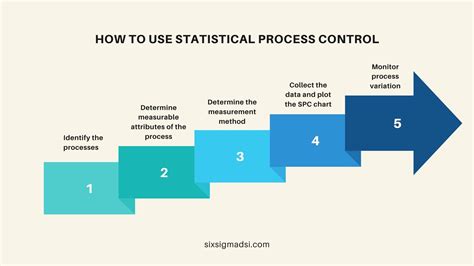
Understanding the Upper Control Limit (UCL) and Lower Control Limit (LCL) formulas is crucial in statistical process control, as they help in determining whether a process is in control or not. Mastering these formulas enables professionals to make informed decisions, detect anomalies, and improve the overall quality of their processes. Here are five ways to master the UCL and LCL formulas:
The Importance of UCL and LCL Formulas
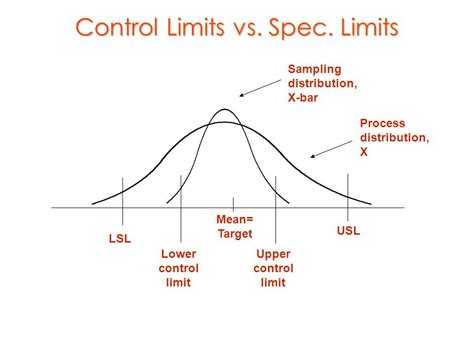
In statistical process control, the UCL and LCL formulas are used to calculate the control limits of a process. These limits determine whether a process is in control or not. The UCL is the upper limit, while the LCL is the lower limit. Any data point that falls outside these limits indicates that the process is out of control.
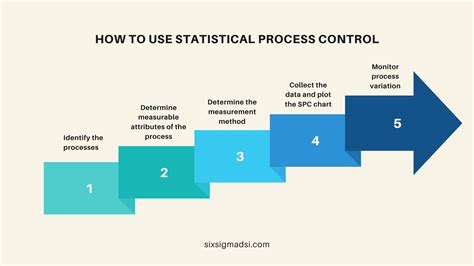
Understanding the UCL and LCL Formulas
The UCL and LCL formulas are as follows:
UCL = X̄ + (3 × σ / √n) LCL = X̄ - (3 × σ / √n)
Where: X̄ = The mean of the sample σ = The standard deviation of the sample n = The sample size
1. Practice with Sample Data
To master the UCL and LCL formulas, it is essential to practice with sample data. Use online calculators or spreadsheet software to calculate the UCL and LCL values. Practice with different sample sizes, means, and standard deviations to understand how the formulas work.
UCL and LCL Formula Example
Suppose we have a sample of 10 data points with a mean of 20 and a standard deviation of 2. To calculate the UCL and LCL, we would use the following formulas:
UCL = 20 + (3 × 2 / √10) = 24.95 LCL = 20 - (3 × 2 / √10) = 15.05

2. Understand the Concept of Sigma
Sigma (σ) is a critical component of the UCL and LCL formulas. It represents the standard deviation of the sample. Understanding the concept of sigma is essential in mastering the UCL and LCL formulas. Sigma measures the amount of variation in the sample data.
What is Sigma?
Sigma is the Greek letter used to represent the standard deviation of a population. It measures the amount of variation in the data. A small sigma value indicates that the data points are close to the mean, while a large sigma value indicates that the data points are spread out.
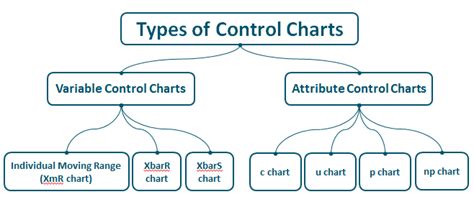
3. Learn About the Different Types of Control Charts
There are several types of control charts used in statistical process control, including:
- X-bar chart
- R-chart
- P-chart
- C-chart
Each type of control chart has its own unique characteristics and uses. Understanding the different types of control charts is essential in mastering the UCL and LCL formulas.
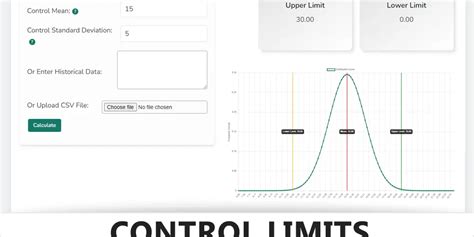
4. Use Online Resources and Calculators
There are many online resources and calculators available that can help you master the UCL and LCL formulas. Use these resources to practice and calculate the UCL and LCL values for different sample data.
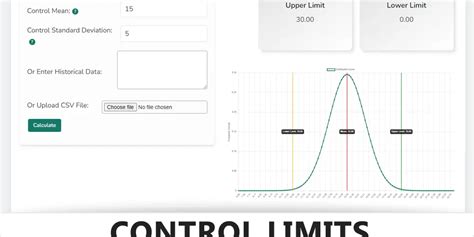
UCL and LCL Calculator
An online calculator can be used to calculate the UCL and LCL values quickly and accurately. Simply enter the sample data, mean, standard deviation, and sample size, and the calculator will provide the UCL and LCL values.
5. Apply the UCL and LCL Formulas in Real-World Scenarios
To master the UCL and LCL formulas, it is essential to apply them in real-world scenarios. Use the formulas to analyze and improve processes in your industry or profession.
Real-World Example
A manufacturing company produces light bulbs with a mean lifespan of 1000 hours and a standard deviation of 50 hours. To determine whether the process is in control, the company calculates the UCL and LCL values using the formulas.
UCL = 1000 + (3 × 50 / √10) = 1095.4 LCL = 1000 - (3 × 50 / √10) = 904.6
The company uses these values to monitor the process and detect any anomalies.
Gallery of UCL and LCL Formula Images
UCL and LCL Formula Image Gallery






Conclusion
Mastering the UCL and LCL formulas requires practice, patience, and persistence. By following these five ways, you can improve your understanding of the UCL and LCL formulas and apply them in real-world scenarios. Remember to practice with sample data, understand the concept of sigma, learn about the different types of control charts, use online resources and calculators, and apply the formulas in real-world scenarios.
