Intro
Boost math skills with 5 expert strategies for mastering volume of irregular figures worksheets. Discover how to break down complex shapes, apply formulas, and visualize dimensions to solve problems with ease. From prism and pyramid volumes to surface area and 3D geometry, conquer irregular shapes with confidence.
Mastering the volume of irregular figures is a crucial skill in mathematics, particularly in geometry and engineering. Irregular figures, also known as non-regular or non-standard shapes, do not have a standard formula for calculating their volume. However, with practice and the right strategies, students can develop their skills in solving volume problems involving irregular figures. In this article, we will explore five ways to master volume of irregular figures worksheets.

Understanding the Basics of Volume of Irregular Figures
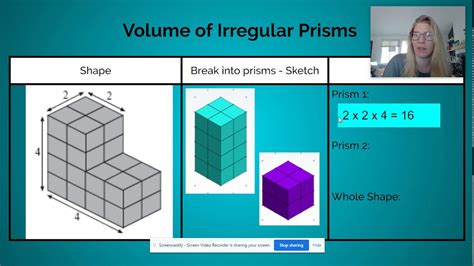
Before diving into the strategies for mastering volume of irregular figures worksheets, it is essential to understand the basics. The volume of an irregular figure can be calculated by dividing the shape into smaller, regular shapes, such as rectangular prisms or triangular prisms, and then calculating the volume of each component. This approach requires a deep understanding of the formulas for the volume of various regular shapes.
Strategy 1: Decompose Irregular Figures into Regular Shapes
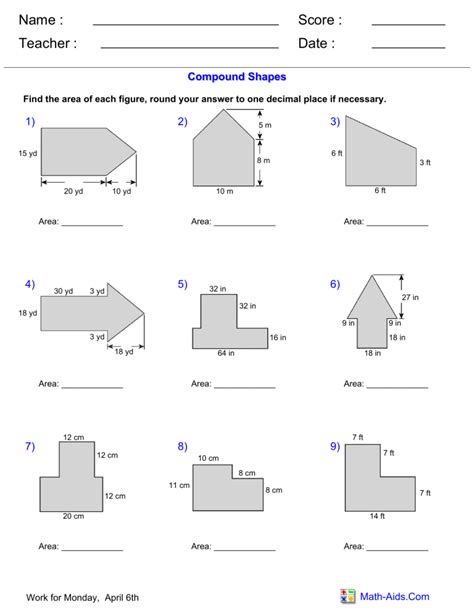
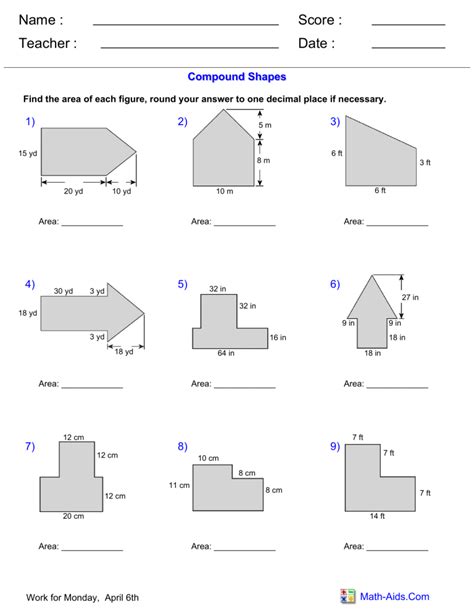
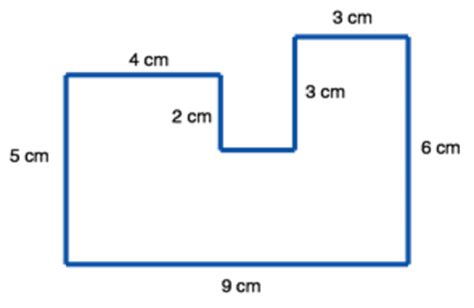
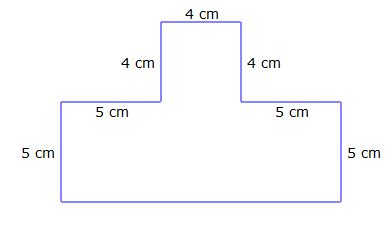
One effective strategy for mastering volume of irregular figures worksheets is to decompose the irregular shape into regular shapes. This approach involves breaking down the irregular shape into smaller, more manageable components, such as rectangular prisms, triangular prisms, or cylinders. Once the irregular shape is decomposed, students can use the formulas for the volume of regular shapes to calculate the volume of each component.
Example: Decomposing an Irregular Shape into Regular Shapes
Suppose we have an irregular shape with a rectangular base and a triangular top. To calculate the volume of this shape, we can decompose it into a rectangular prism and a triangular prism. The volume of the rectangular prism can be calculated using the formula V = lwh, where l is the length, w is the width, and h is the height. The volume of the triangular prism can be calculated using the formula V = (1/2)bh, where b is the base and h is the height.
Strategy 2: Use the Dissection Method
Another strategy for mastering volume of irregular figures worksheets is to use the dissection method. This approach involves dissecting the irregular shape into smaller, more manageable components, such as pyramids or cones. Once the irregular shape is dissected, students can use the formulas for the volume of regular shapes to calculate the volume of each component.
Example: Using the Dissection Method
Suppose we have an irregular shape with a square base and a pyramidal top. To calculate the volume of this shape, we can dissect it into a square pyramid. The volume of the square pyramid can be calculated using the formula V = (1/3)Bh, where B is the base and h is the height.
Strategy 3: Use the Cavalieri's Principle
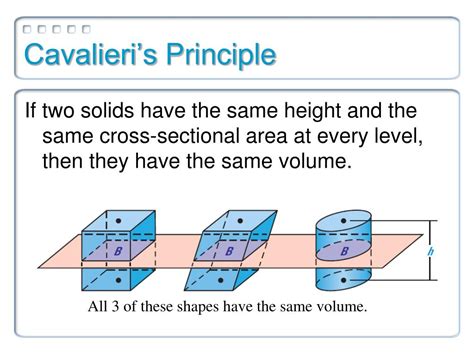
Cavalieri's Principle is a powerful tool for calculating the volume of irregular figures. This principle states that if two shapes have the same height and the same cross-sectional area at every height, then they have the same volume. By applying Cavalieri's Principle, students can calculate the volume of irregular figures by comparing them to regular shapes with known volumes.
Example: Using Cavalieri's Principle
Suppose we have an irregular shape with a triangular base and a rectangular top. To calculate the volume of this shape, we can compare it to a rectangular prism with the same height and cross-sectional area. By applying Cavalieri's Principle, we can calculate the volume of the irregular shape.
Strategy 4: Use the Method of Shells
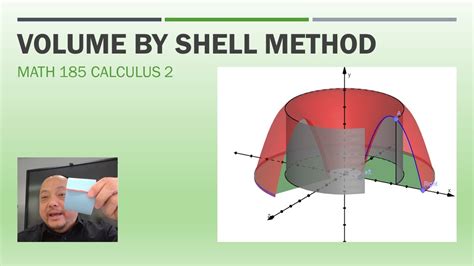
The method of shells is another powerful tool for calculating the volume of irregular figures. This method involves calculating the volume of a shape by summing up the volumes of infinitesimally thin shells that make up the shape. By applying the method of shells, students can calculate the volume of irregular figures with complex boundaries.
Example: Using the Method of Shells
Suppose we have an irregular shape with a circular base and a curved top. To calculate the volume of this shape, we can use the method of shells. By summing up the volumes of infinitesimally thin shells that make up the shape, we can calculate the volume of the irregular shape.
Strategy 5: Practice, Practice, Practice
Finally, the key to mastering volume of irregular figures worksheets is practice. Students should practice solving a variety of problems involving irregular figures, using different strategies and techniques. By practicing regularly, students can develop their skills and build their confidence in solving volume problems involving irregular figures.
Conclusion
Mastering the volume of irregular figures is a crucial skill in mathematics, particularly in geometry and engineering. By using the five strategies outlined above, students can develop their skills in solving volume problems involving irregular figures. Remember, practice is key, so be sure to practice regularly to build your confidence and skills.
Irregular Figures Image Gallery


We hope this article has been helpful in providing strategies for mastering volume of irregular figures worksheets. Remember to practice regularly and build your skills in solving volume problems involving irregular figures.
