Z Score Practice Worksheet With Solutions And Examples

Understanding the concept of z scores is crucial in statistics, as it helps in comparing data points to their mean and standard deviation. In this article, we will delve into the world of z scores, provide practice worksheets, and offer solutions and examples to help solidify your understanding.

What is a Z Score?

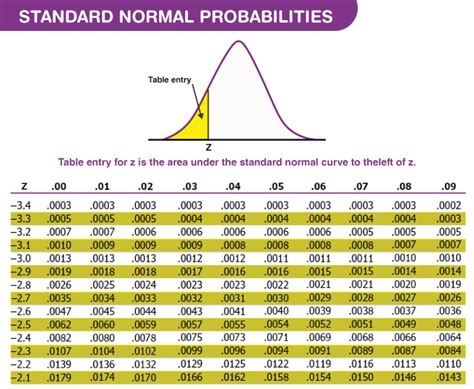
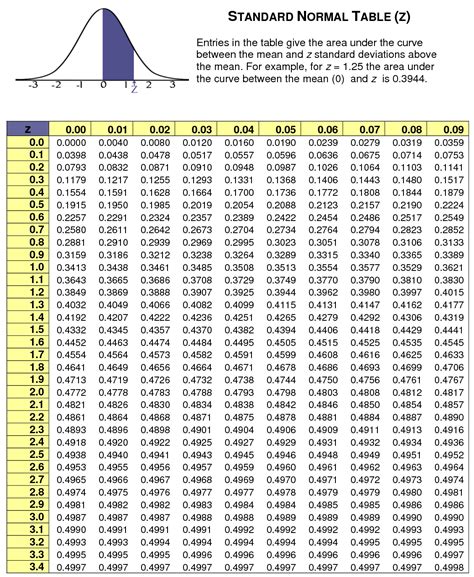
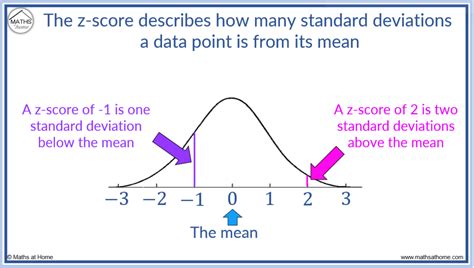
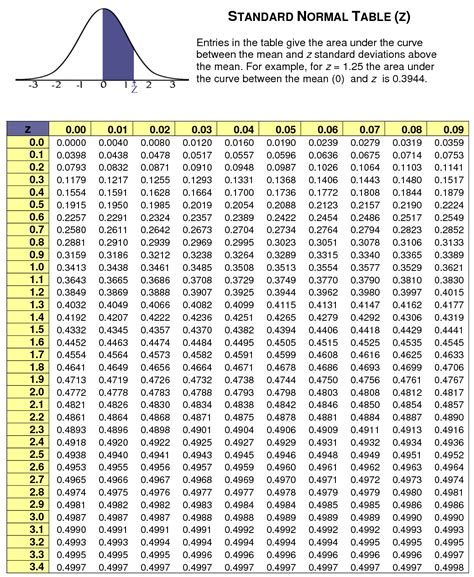
A z score, also known as a standard score, is a dimensionless quantity that indicates how many standard deviations an element is from the mean. The z score is calculated using the following formula:

z = (X - μ) / σ

where X is the data point, μ is the mean, and σ is the standard deviation.

Interpretation of Z Scores

The interpretation of z scores is crucial in understanding the relative position of a data point within a dataset. Here are some key takeaways:

• A z score of 0 indicates that the data point is equal to the mean.
• A positive z score indicates that the data point is above the mean, while a negative z score indicates that it is below the mean.
• The larger the absolute value of the z score, the farther away the data point is from the mean.

Z Score Practice Worksheet

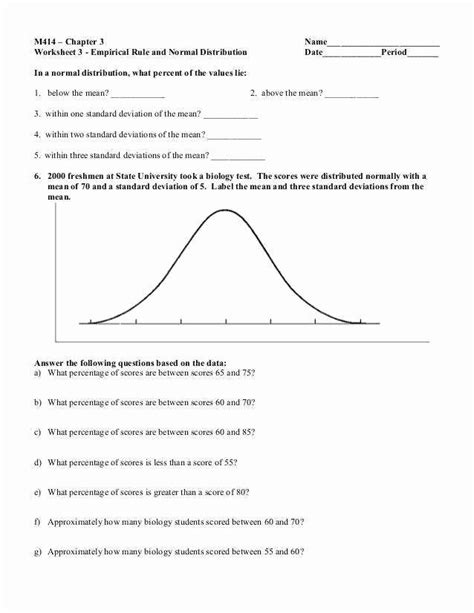
Here's a practice worksheet to help you solidify your understanding of z scores:

Section 1: Calculating Z Scores

1. Calculate the z score for a data point of 25, given a mean of 20 and a standard deviation of 5.
2. Calculate the z score for a data point of 10, given a mean of 15 and a standard deviation of 3.
3. Calculate the z score for a data point of 30, given a mean of 25 and a standard deviation of 2.

Section 2: Interpreting Z Scores

1. A data point has a z score of -2. What does this indicate about the data point's position relative to the mean?
2. A data point has a z score of 3. What does this indicate about the data point's position relative to the mean?
3. A data point has a z score of 0. What does this indicate about the data point's position relative to the mean?

Solutions and Examples

Here are the solutions and examples to help you better understand z scores:

Section 1: Calculating Z Scores

1. z = (25 - 20) / 5 = 1
2. z = (10 - 15) / 3 = -1.67
3. z = (30 - 25) / 2 = 2.5

Section 2: Interpreting Z Scores

1. A z score of -2 indicates that the data point is 2 standard deviations below the mean.
2. A z score of 3 indicates that the data point is 3 standard deviations above the mean.
3. A z score of 0 indicates that the data point is equal to the mean.

Real-World Applications of Z Scores

Z scores have numerous real-world applications, including:

• Predicting stock prices
• Analyzing medical data
• Evaluating student performance
• Determining credit scores

Gallery of Z Score-Related Images

Z Score Image Gallery

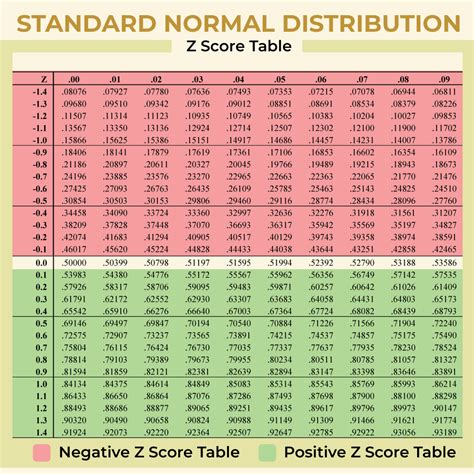
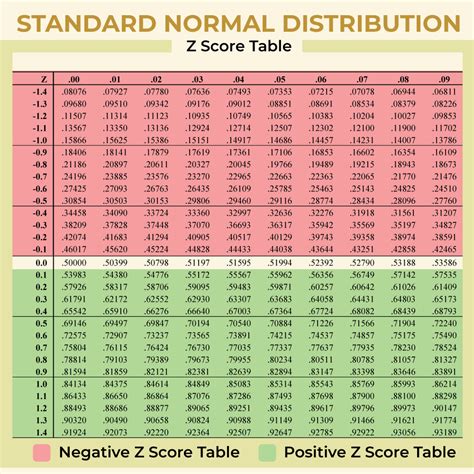
We hope this article has provided you with a comprehensive understanding of z scores, including how to calculate them, interpret them, and apply them in real-world scenarios. Remember to practice using the practice worksheet and solutions provided to solidify your understanding. Share your thoughts and questions in the comments below!