7 Steps To Master Binomial Option Pricing In Excel

Unlocking the Power of Binomial Option Pricing in Excel

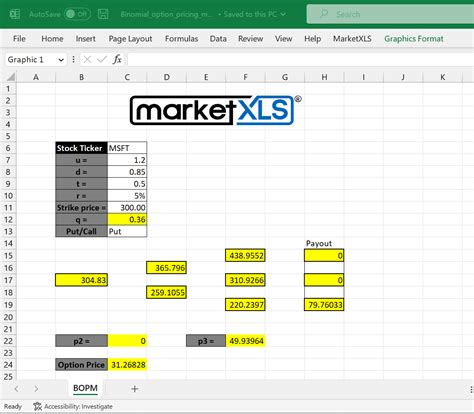
Options are a type of financial derivative that give the holder the right, but not the obligation, to buy or sell an underlying asset at a predetermined price. Accurately pricing options is crucial for investors, traders, and financial institutions. One popular method for pricing options is the binomial option pricing model. In this article, we will explore the 7 steps to master binomial option pricing in Excel.

Understanding the Binomial Option Pricing Model

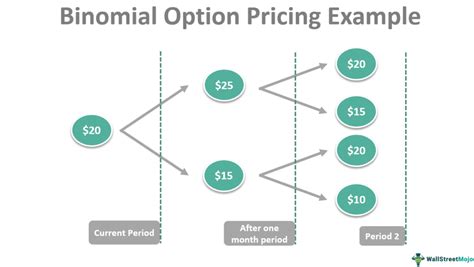
The binomial option pricing model is a discrete-time model that assumes the price of the underlying asset can only move up or down by a certain percentage at each time step. This model is based on the idea that the price of the underlying asset follows a binomial distribution, hence the name. The model is widely used due to its simplicity and accuracy.

Advantages of the Binomial Option Pricing Model

• Easy to implement and understand
• Accurate for short-term options
• Can handle complex payoffs
• Can be extended to more complex models

Step 1: Set Up the Model Parameters

To start, we need to set up the model parameters. These include the underlying asset price, strike price, risk-free interest rate, time to maturity, and volatility. We will use these parameters to calculate the up and down factors, which determine the possible price movements of the underlying asset.

Model Parameters

• Underlying asset price (S)
• Strike price (K)
• Risk-free interest rate (r)
• Time to maturity (T)
• Volatility (σ)

Step 2: Calculate the Up and Down Factors

The up and down factors are calculated using the following formulas:

Up factor (u) = e^(σ * √t) Down factor (d) = 1 / u

where t is the time step.

Calculating the Up and Down Factors in Excel

	A	B	C
1	S	K	r
2	σ	T	t
3	u	d

Formula: =EXP($C$2*SQRT($C$3)) (up factor) Formula: =1/A3 (down factor)

Step 3: Create the Binomial Tree

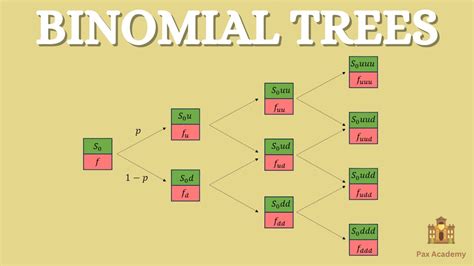
The binomial tree is a graphical representation of the possible price movements of the underlying asset. We will use the up and down factors to create the tree.

Creating the Binomial Tree in Excel

	A	B	C	D
1	S	u	d
2	S*u	S*d
3	S*u^2	Sud	S*d^2

Formula: =$A$1A2 (up movement) Formula: =$A$1B2 (down movement)

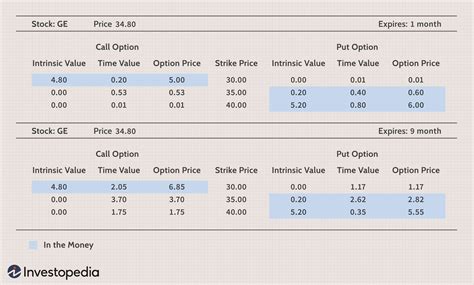
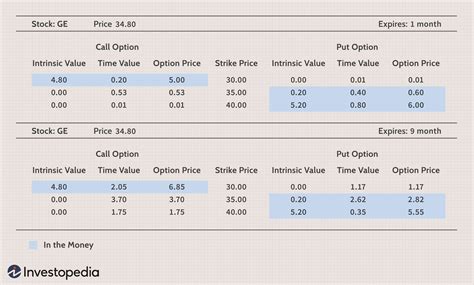
Step 4: Calculate the Option Values

We will use the binomial tree to calculate the option values. We will start at the final time step and work backwards to the present.

Calculating the Option Values in Excel

	A	B	C	D
1	S	u	d
2	S*u	S*d
3	S*u^2	Sud	S*d^2
4				V

Formula: =MAX($A$1-$B$1,0) (option value at expiration) Formula: =(1/2)*($A$1+$B$1) (option value at previous time step)

Step 5: Calculate the Risk-Neutral Probabilities

The risk-neutral probabilities are used to calculate the expected value of the option. We will use the following formulas:

p = (e^(rt) - d) / (u - d) 1 - p = (u - e^(rt)) / (u - d)

Calculating the Risk-Neutral Probabilities in Excel

	A	B	C
1	r	t	u
2	d	p	1-p
3

Formula: =(EXP($A$1*$B$1)-$B$2)/($A$3-$B$2) (risk-neutral probability) Formula: =($A$3-EXP($A$1*$B$1))/($A$3-$B$2) (1 - risk-neutral probability)

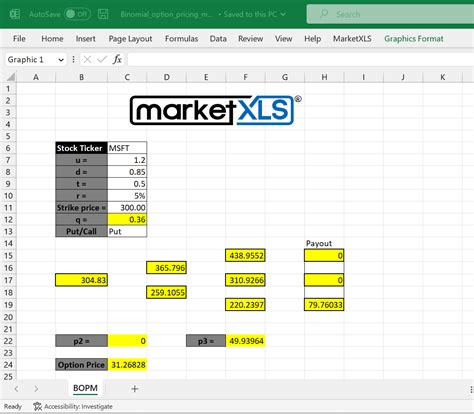
Step 6: Calculate the Option Price

We will use the risk-neutral probabilities and the option values to calculate the option price.

Calculating the Option Price in Excel

	A	B	C	D
1	S	u	d
2	S*u	S*d
3	S*u^2	Sud	S*d^2
4				V
5				P

Formula: =($A$1*$B$5+($C$1-$A$1)$B$5)/EXP($A$1$B$2) (option price)

Step 7: Verify the Results

We will verify the results by comparing the calculated option price with the actual market price.

Verifying the Results in Excel

	A	B
1	S	P
2

Formula: =ABS($A$1-$B$1) (absolute difference)

By following these 7 steps, you can master the binomial option pricing model in Excel. Remember to verify your results and adjust the model parameters as necessary.

---

Binomial Option Pricing in Excel Image Gallery

We hope this article has helped you master the binomial option pricing model in Excel. If you have any questions or need further clarification, please leave a comment below. Share this article with your friends and colleagues who may benefit from it.