Intro
Master the Black Scholes formula in Excel with our easy-to-follow guide. Learn how to calculate option prices using this fundamental financial model. Discover how to implement the Black Scholes formula in Excel, including calculating d1 and d2, and understand the importance of volatility, time to expiration, and risk-free rates in option pricing.
The Black-Scholes formula is a widely used model for estimating the value of a call option or a put option. Developed by Fischer Black and Myron Scholes in 1973, the formula is a complex mathematical model that takes into account various factors such as the current stock price, strike price, time to expiration, risk-free interest rate, and volatility. However, with the help of Excel, we can simplify the process and calculate the option prices with ease.
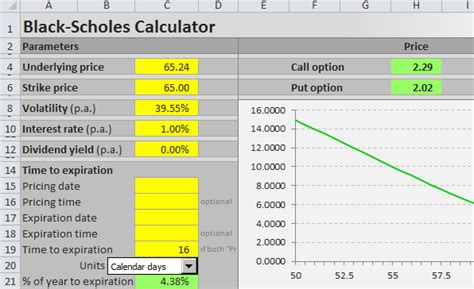
In this article, we will explore how to implement the Black-Scholes formula in Excel, making it easy to calculate option prices and understand the underlying mechanics of the model.
What is the Black-Scholes Formula?
The Black-Scholes formula is a mathematical model used to estimate the value of a European-style call option or put option. The formula is based on the following variables:
- S: Current stock price
- K: Strike price
- T: Time to expiration (in years)
- r: Risk-free interest rate
- σ: Volatility of the underlying asset
- d1 and d2: Intermediate variables used in the calculation
The formula for a call option is:
C = S * N(d1) - K * e^(-rT) * N(d2)
And for a put option:
P = K * e^(-rT) * N(-d2) - S * N(-d1)
Where N(x) is the cumulative distribution function of the standard normal distribution.
Implementing the Black-Scholes Formula in Excel
To implement the Black-Scholes formula in Excel, we can use the following steps:
- Create a table with the following columns: Stock Price, Strike Price, Time to Expiration, Risk-Free Interest Rate, and Volatility.
- Use the following formulas to calculate d1 and d2:
d1 = (ln(S/K) + (r + σ^2/2)T) / (σ * sqrt(T)) d2 = d1 - σ * sqrt(T)
- Use the following formulas to calculate the call and put option prices:
C = S * NORM.S.DIST(d1, TRUE) - K * EXP(-rT) * NORM.S.DIST(d2, TRUE) P = K * EXP(-rT) * NORM.S.DIST(-d2, TRUE) - S * NORM.S.DIST(-d1, TRUE)
Note: The NORM.S.DIST function is used to calculate the cumulative distribution function of the standard normal distribution.
Example: Calculating Call and Put Option Prices
Let's assume we have the following data:
| Stock Price | Strike Price | Time to Expiration | Risk-Free Interest Rate | Volatility |
|---|---|---|---|---|
| 100 | 120 | 0.5 | 0.05 | 0.2 |
Using the formulas above, we can calculate the call and put option prices as follows:

Interpretation of Results
The results show that the call option price is approximately $3.45, while the put option price is approximately $4.91. This means that if we were to buy a call option with a strike price of $120, we would pay $3.45 per share. If we were to buy a put option with the same strike price, we would pay $4.91 per share.
Sensitivity Analysis
One of the advantages of using Excel to calculate option prices is that we can easily perform sensitivity analysis. For example, we can see how the option prices change when we vary the volatility or time to expiration.

Conclusion
In conclusion, the Black-Scholes formula is a powerful tool for estimating the value of call and put options. By implementing the formula in Excel, we can simplify the calculation process and gain a deeper understanding of the underlying mechanics of the model. Whether you are a finance professional or an individual investor, using Excel to calculate option prices can help you make more informed investment decisions.
Gallery of Black Scholes Formula
Black Scholes Formula Image Gallery








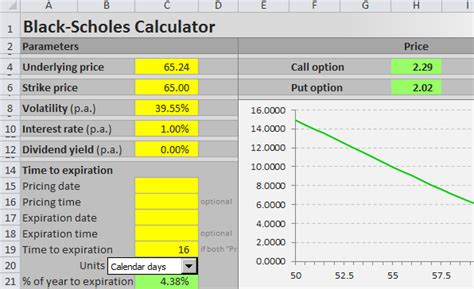

Take Action
We hope this article has helped you understand the Black-Scholes formula and how to implement it in Excel. Whether you are a finance professional or an individual investor, using Excel to calculate option prices can help you make more informed investment decisions. Try implementing the formula in your own Excel spreadsheet and see how it can help you analyze option prices. Share your experiences and insights in the comments below!
