Intro
Master Chomsky Normal Form with 5 expert tips, simplifying context-free grammars and parse trees for efficient language processing and compiler design, using production rules and syntax analysis.
The Chomsky Normal Form (CNF) is a fundamental concept in the field of formal language theory and computer science. It is a specific format for context-free grammars, which are used to define the structure of languages. Understanding CNF is crucial for various applications, including compiler design, natural language processing, and formal language theory. In this article, we will delve into the world of CNF, exploring its importance, benefits, and providing valuable tips for working with it.
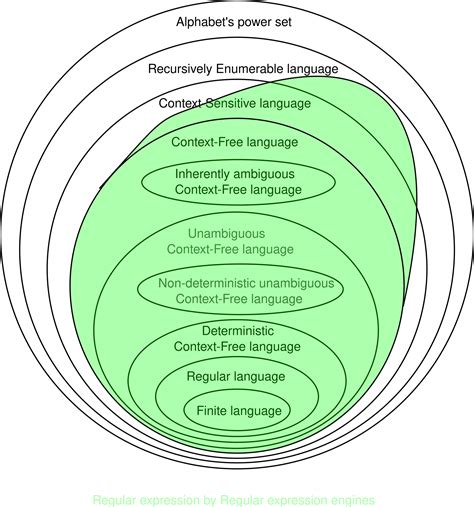
The study of formal languages and their properties has been a cornerstone of computer science since its inception. The Chomsky hierarchy, proposed by Noam Chomsky, categorizes languages based on their generative power, with regular languages being the simplest and recursively enumerable languages being the most complex. Context-free languages, which can be generated by context-free grammars, are of particular interest due to their balance between simplicity and expressiveness. The Chomsky Normal Form is a standardized way of representing these grammars, making them easier to analyze and work with.
The significance of CNF lies in its ability to simplify the analysis and processing of context-free languages. By converting a context-free grammar into CNF, one can more easily determine properties of the language, such as whether a given string belongs to the language (membership problem) or whether the language is empty (emptiness problem). Moreover, many algorithms in compiler design and natural language processing rely on grammars being in CNF, as it facilitates the parsing process and the analysis of language structures.
Introduction to Chomsky Normal Form

To understand CNF, one must first grasp the basics of context-free grammars. A context-free grammar consists of a set of non-terminal symbols, terminal symbols, production rules, and a start symbol. The production rules define how non-terminal symbols can be replaced by sequences of terminal and non-terminal symbols. A grammar is in Chomsky Normal Form if all its production rules are of the form A → BC or A → a, where A, B, and C are non-terminal symbols, and a is a terminal symbol. This restriction simplifies the grammar, making it more manageable for theoretical analysis and practical applications.
Benefits of Chomsky Normal Form

The benefits of converting a context-free grammar into CNF are numerous. Firstly, it enables the use of specific algorithms designed for CNF grammars, which can solve problems related to language recognition and parsing more efficiently. Secondly, CNF facilitates the comparison and analysis of different grammars, as it provides a standardized format. This standardization is crucial for theoretical studies, where the properties of languages and grammars need to be compared and analyzed systematically.
Working with Chomsky Normal Form
Working with CNF involves understanding the process of converting a given context-free grammar into this standard form. The conversion process typically involves several steps, including removing useless symbols, removing epsilon productions, removing unit productions, and finally, converting the remaining productions into the appropriate form. Each step requires careful analysis and application of specific rules to ensure that the resulting grammar is equivalent to the original one but in CNF.
Tips for Converting to Chomsky Normal Form

Here are some valuable tips for converting a context-free grammar to CNF:
- Start by removing useless symbols: Useless symbols are those that cannot be derived from the start symbol or cannot derive any terminal strings. Removing them simplifies the grammar without affecting the language it generates.
- Eliminate epsilon productions: Epsilon productions are rules of the form A → ε, where ε represents the empty string. These can be removed by carefully analyzing the grammar and applying specific algorithms designed for this purpose.
- Remove unit productions: Unit productions are of the form A → B, where A and B are non-terminal symbols. Removing these involves substituting the unit production with the actual production that B can derive.
- Convert to CNF: After the above steps, the remaining task is to convert the production rules into the CNF, which involves ensuring that all rules are either of the form A → BC or A → a.
Applications of Chomsky Normal Form

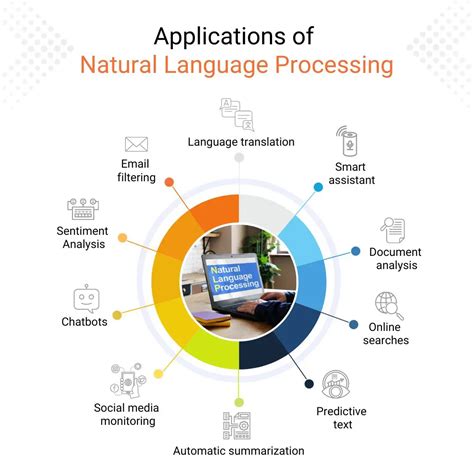
The applications of CNF are diverse and significant. In compiler design, CNF is used in the parsing phase to analyze the source code and ensure it conforms to the language's syntax. In natural language processing, CNF can be applied to model the grammatical structure of sentences, facilitating tasks such as language translation and text analysis. Furthermore, CNF plays a crucial role in theoretical computer science, particularly in the study of formal languages and automata theory.
Common Challenges and Solutions
One of the common challenges when working with CNF is ensuring that the conversion process does not alter the language generated by the original grammar. This requires a deep understanding of the conversion algorithms and careful application of the rules. Another challenge is dealing with complex grammars that have a large number of production rules and symbols. In such cases, using automated tools or software that can perform the conversion to CNF can be highly beneficial.
Best Practices for Working with CNF

Best practices for working with CNF include:
- Understand the basics: Before diving into complex grammars, ensure a solid grasp of context-free grammars and the conversion process to CNF.
- Use systematic approaches: When converting a grammar to CNF, follow a systematic approach to avoid errors and ensure that all necessary steps are taken.
- Leverage technology: Utilize software tools or programming libraries that can assist in the conversion process, especially for large and complex grammars.
- Test and validate: After converting a grammar to CNF, test it with sample inputs to validate that it generates the same language as the original grammar.
Future Directions and Research

Future research directions in the area of CNF and formal language theory include exploring more efficient algorithms for converting grammars to CNF, developing new applications of CNF in areas such as artificial intelligence and data science, and investigating the theoretical limits of CNF in terms of its expressive power and computational complexity. Additionally, there is a growing interest in applying formal language theory to real-world problems, such as modeling biological systems and analyzing network protocols, which could benefit from advancements in CNF and related areas.
Chomsky Normal Form Image Gallery







In conclusion, the Chomsky Normal Form is a powerful tool in the field of formal language theory, offering a standardized way to represent context-free grammars. Its applications are diverse, ranging from compiler design and natural language processing to theoretical computer science. By understanding the importance of CNF, its benefits, and how to work with it effectively, researchers and practitioners can leverage its potential to advance our understanding of languages and develop more sophisticated language processing technologies. We invite readers to share their thoughts and experiences with CNF, and we look forward to continuing the discussion on the applications and future directions of this fundamental concept in computer science.
