5 Ways To Apply Empirical Rule Formula In Excel

Are you tired of dealing with complex statistical calculations in Excel? Do you struggle to apply the empirical rule formula to your data? Look no further! In this article, we will explore five ways to apply the empirical rule formula in Excel, making it easier for you to analyze and understand your data.

The empirical rule, also known as the 68-95-99.7 rule, states that about 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations. This rule is useful for understanding the distribution of your data and making predictions.

Understanding the Empirical Rule Formula

Before we dive into the ways to apply the empirical rule formula in Excel, let's first understand the formula itself. The empirical rule formula is based on the mean and standard deviation of your data. The formula is:

Mean ± (Standard Deviation x Number of Standard Deviations)

For example, if you want to calculate the range of values that fall within one standard deviation of the mean, you would use the formula:

Mean ± (Standard Deviation x 1)

Method 1: Using the AVERAGE and STDEV Functions

One way to apply the empirical rule formula in Excel is by using the AVERAGE and STDEV functions. These functions calculate the mean and standard deviation of your data, respectively.

1. Select the cell where you want to calculate the mean.
2. Type "=AVERAGE(range)" and press Enter.
3. Select the cell where you want to calculate the standard deviation.
4. Type "=STDEV(range)" and press Enter.
5. Use the mean and standard deviation values to calculate the range of values that fall within one, two, or three standard deviations of the mean.

Example: Applying the Empirical Rule Formula Using AVERAGE and STDEV

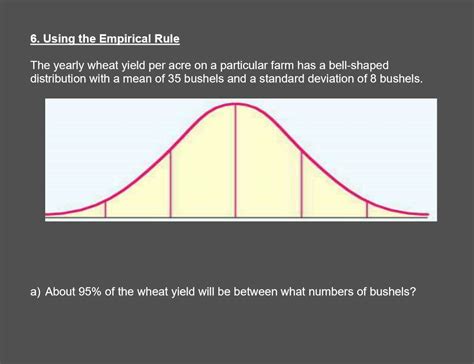
Suppose we have a dataset of exam scores, and we want to calculate the range of scores that fall within one standard deviation of the mean.

Score
80
70
90
85
75

Using the AVERAGE function, we calculate the mean score to be 80. Using the STDEV function, we calculate the standard deviation to be 5.41.

To calculate the range of scores that fall within one standard deviation of the mean, we use the formula:

80 ± (5.41 x 1)

This gives us a range of scores from 74.59 to 85.41.

Method 2: Using the NORM.S.DIST Function

Another way to apply the empirical rule formula in Excel is by using the NORM.S.DIST function. This function calculates the cumulative distribution function of the standard normal distribution.

1. Select the cell where you want to calculate the probability.
2. Type "=NORM.S.DIST(x, mean, standard_dev, cumulative)" and press Enter.
3. Replace x with the value you want to calculate the probability for.
4. Replace mean with the mean value.
5. Replace standard_dev with the standard deviation value.
6. Set cumulative to TRUE.

Example: Applying the Empirical Rule Formula Using NORM.S.DIST

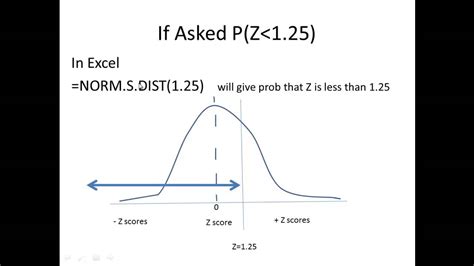
Suppose we want to calculate the probability that a student will score between 70 and 90 on the exam.

Using the NORM.S.DIST function, we calculate the probability as follows:

=NORM.S.DIST(90, 80, 5.41, TRUE) - NORM.S.DIST(70, 80, 5.41, TRUE)

This gives us a probability of 0.6827, which means that about 68.27% of the students will score between 70 and 90.

Method 3: Using the STDEV.S Function

If you are using Excel 2013 or later, you can use the STDEV.S function to calculate the standard deviation of your data.

1. Select the cell where you want to calculate the standard deviation.
2. Type "=STDEV.S(range)" and press Enter.

This function calculates the sample standard deviation, which is more accurate for small datasets.

Method 4: Using the Empirical Rule Formula in VBA

If you prefer to use VBA, you can create a macro that applies the empirical rule formula to your data.

1. Open the Visual Basic Editor.
2. Create a new module.
3. Paste the following code:

Sub EmpiricalRule()
  Dim mean As Double
  Dim stdDev As Double
  Dim range As Range
  
  Set range = Selection
  
  mean = Application.WorksheetFunction.Average(range)
  stdDev = Application.WorksheetFunction.StDev(range)
  
  MsgBox "The range of values that fall within one standard deviation of the mean is: " & mean - stdDev & " to " & mean + stdDev
End Sub

4. Run the macro.

This macro calculates the mean and standard deviation of your data and then displays the range of values that fall within one standard deviation of the mean.

Method 5: Using the Analysis ToolPak

Finally, you can use the Analysis ToolPak to apply the empirical rule formula to your data.

1. Go to the Data tab.
2. Click on Data Analysis.
3. Select the Descriptive Statistics option.
4. Select the range of cells that you want to analyze.
5. Click OK.

This will generate a report that includes the mean, standard deviation, and other statistical measures.

Empirical Rule Formula Image Gallery

We hope this article has helped you understand how to apply the empirical rule formula in Excel. Whether you use the AVERAGE and STDEV functions, the NORM.S.DIST function, or VBA, you can easily calculate the range of values that fall within one, two, or three standard deviations of the mean.

What's your favorite way to apply the empirical rule formula in Excel? Share your thoughts and experiences in the comments below!