Discover fascinating 7 Cube Facts, exploring cube geometry, properties, and real-world applications, including spatial reasoning, math concepts, and 3D structures.
The cube is one of the most fascinating and versatile shapes in geometry, with a wide range of applications in mathematics, science, art, and design. From its unique properties to its role in popular culture, there's more to the cube than meets the eye. In this article, we'll delve into the world of cubes, exploring their characteristics, uses, and intriguing facts. Whether you're a math enthusiast, a design aficionado, or simply someone who appreciates the beauty of geometry, you'll find something to captivate your interest.
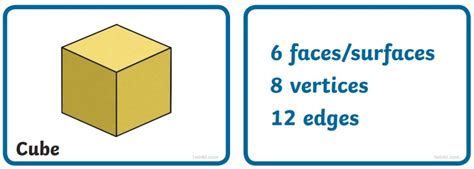
Cubes have been a part of human culture for thousands of years, with ancient civilizations such as the Egyptians and Greeks using them in their architecture and art. The cube's simplicity and symmetry make it a compelling shape, both aesthetically and mathematically. Its six identical square faces, twelve edges, and eight vertices create a sense of balance and harmony, which has inspired countless artists, designers, and architects throughout history. From the pyramids of Giza to the modernist skyscrapers of today, the cube has played a significant role in shaping our built environment.
The cube's unique properties also make it an essential shape in mathematics and science. Its volume, surface area, and diagonal lengths can be calculated using simple formulas, making it a fundamental shape in geometry and trigonometry. The cube's symmetry also makes it a crucial shape in group theory, a branch of mathematics that studies the symmetries of objects. In physics, the cube is used to model the structure of crystals and the behavior of particles in three-dimensional space. Whether you're a student of mathematics or a scientist, the cube is an indispensable shape that can help you understand complex concepts and phenomena.
Properties of a Cube
Types of Cubes
There are several types of cubes, each with its own unique properties and characteristics. A unit cube is a cube with edges of length one, which is often used as a reference cube in mathematics and science. A cube can also be classified as a regular cube, which means that all its faces are identical squares, or an irregular cube, which means that its faces are not identical. A cube can also be a rectangular cube, which is a cube with rectangular faces, or a triangular cube, which is a cube with triangular faces.Cube in Mathematics
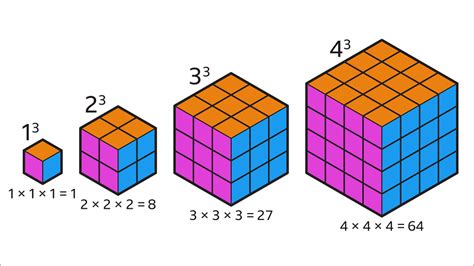
Calculating Cube Volume and Surface Area
Calculating the volume and surface area of a cube is a straightforward process that involves using simple formulas. The volume of a cube is calculated by cubing the length of one of its edges, while its surface area is calculated by finding the area of one face and multiplying it by six. For example, if a cube has an edge length of 5 cm, its volume would be 5^3 = 125 cm^3, and its surface area would be 6 x 5^2 = 150 cm^2.Cube in Art and Design

Cube in Popular Culture
The cube has also appeared in popular culture, with references to the shape appearing in music, film, and literature. The cube is often used as a symbol of simplicity, elegance, and perfection, with many artists and designers using it as a metaphor for their creative vision. The cube has also been featured in various forms of media, including films, video games, and music videos, where it is often used to represent a sense of futurism and technological advancement.Cube Facts and Trivia

Real-World Applications of Cubes
Cubes have a wide range of real-world applications, from architecture and engineering to art and design. The cube's simplicity and symmetry make it a versatile shape that can be used in various contexts, from the design of buildings and bridges to the creation of sculptures and installations. The cube's unique properties also make it a crucial shape in mathematical modeling and problem-solving, with many scientists and engineers using it to understand complex phenomena and systems.Cube Gallery

Cube Image Gallery








Final Thoughts

