Function Or Not Worksheet: Identify And Practice With Ease

Identifying functions in mathematics is a crucial skill, especially in algebra and calculus. It can be a challenging concept for some students, but with practice and the right resources, it can become easier to grasp. In this article, we will explore what functions are, how to identify them, and provide you with a worksheet to practice.

What is a Function?

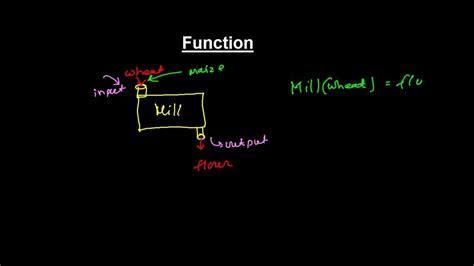
A function is a relation between a set of inputs, called the domain, and a set of possible outputs, called the range. It is a way of describing a relationship between variables, where each input corresponds to exactly one output. In other words, a function is a rule that assigns to each element in the domain exactly one element in the range.

Types of Functions

There are several types of functions, including:

• Linear functions: These are functions that can be represented by a straight line, such as f(x) = 2x + 3.
• Quadratic functions: These are functions that can be represented by a parabola, such as f(x) = x^2 + 4x + 4.
• Polynomial functions: These are functions that can be represented by a polynomial expression, such as f(x) = x^3 + 2x^2 - 7x + 1.
• Rational functions: These are functions that can be represented by a fraction of two polynomials, such as f(x) = (x + 1) / (x - 2).

How to Identify Functions

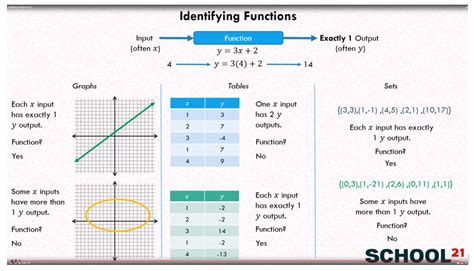
To identify a function, you need to check if it satisfies the following conditions:

• Each input corresponds to exactly one output.
• The relation is well-defined, meaning that it is clear what output corresponds to each input.

Here are some examples to help you practice identifying functions:

• Is the relation {(1, 2), (2, 3), (3, 4)} a function? Yes, because each input corresponds to exactly one output.
• Is the relation {(1, 2), (2, 3), (2, 4)} a function? No, because the input 2 corresponds to two different outputs.

Function Notation

Function notation is a way of writing functions using the notation f(x) = y, where f is the name of the function, x is the input, and y is the output. For example, the function f(x) = 2x + 1 can be read as "f of x is equal to 2x plus 1".

Function Operations

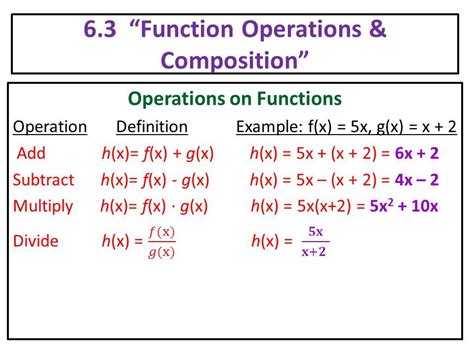
Functions can be combined using various operations, such as addition, subtraction, multiplication, and division. For example, if we have two functions f(x) = 2x + 1 and g(x) = x - 2, we can add them to get a new function (f + g)(x) = 3x - 1.

Function Composition

Function composition is a way of combining two functions to get a new function. For example, if we have two functions f(x) = 2x + 1 and g(x) = x - 2, we can compose them to get a new function (f ∘ g)(x) = f(g(x)) = 2(x - 2) + 1 = 2x - 3.

Worksheet: Identify and Practice with Ease

Here is a worksheet with 10 questions to help you practice identifying and working with functions:

1. Is the relation {(1, 2), (2, 3), (3, 4)} a function? Why or why not?
2. Is the relation {(1, 2), (2, 3), (2, 4)} a function? Why or why not?
3. What is the domain and range of the function f(x) = 2x + 1?
4. What is the inverse of the function f(x) = 2x + 1?
5. If we have two functions f(x) = 2x + 1 and g(x) = x - 2, what is the sum of the two functions?
6. If we have two functions f(x) = 2x + 1 and g(x) = x - 2, what is the product of the two functions?
7. If we have two functions f(x) = 2x + 1 and g(x) = x - 2, what is the composition of the two functions?
8. Is the function f(x) = x^2 + 4x + 4 a quadratic function? Why or why not?
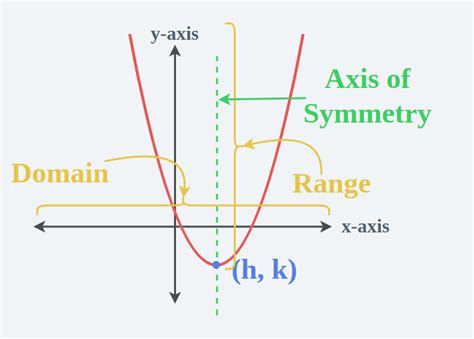
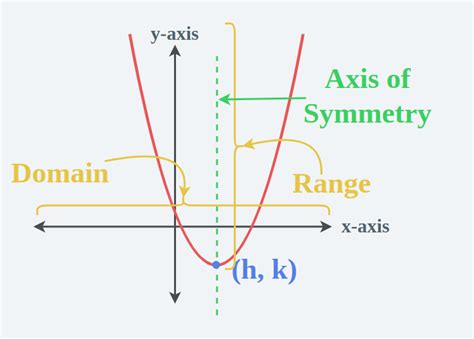
9. What is the vertex of the parabola represented by the function f(x) = x^2 + 4x + 4?
10. What is the axis of symmetry of the parabola represented by the function f(x) = x^2 + 4x + 4?

Function Image Gallery

We hope this worksheet and article have helped you understand and identify functions with ease. Remember to practice regularly and use the resources provided to improve your skills. If you have any questions or need further clarification, please don't hesitate to ask.