Intro
Learn how to find UCL and LCL in Excel with ease. Discover the step-by-step process to calculate upper and lower control limits for quality control and statistical analysis. Master the formulas and functions to identify UCL and LCL, and improve your data-driven decision making with Excels powerful tools.
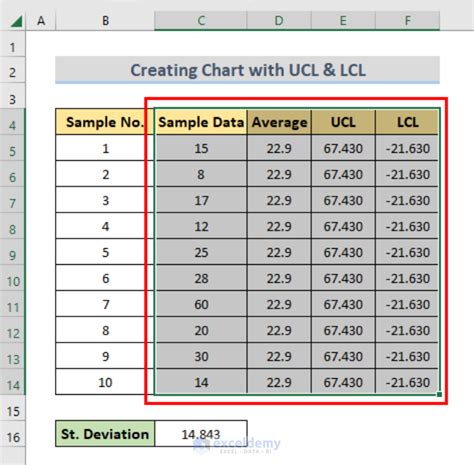
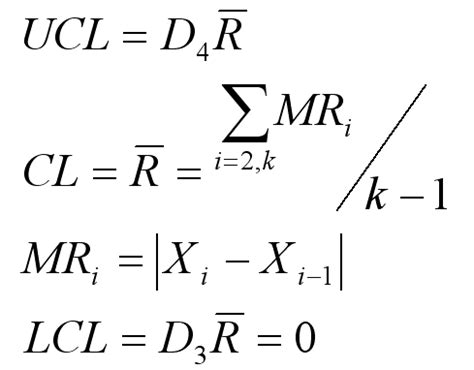Upper and lower control limits (UCL and LCL) are statistical measures used to monitor and control processes in various industries, including manufacturing, healthcare, and finance. These limits help determine whether a process is in control or not. Calculating UCL and LCL in Excel can be a straightforward process if you understand the formulas and concepts involved.
Understanding Control Limits
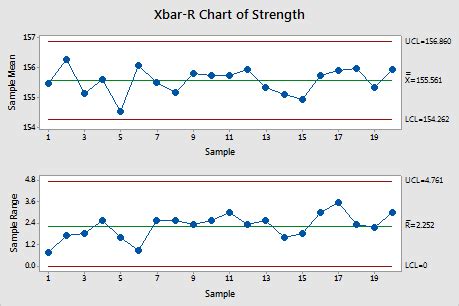
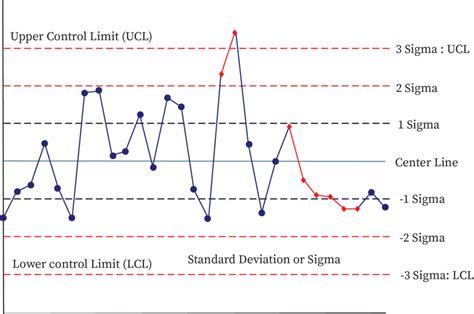
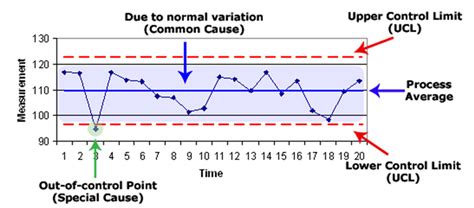
Control limits are used to monitor the performance of a process over time. The upper control limit (UCL) is the maximum value that a process can reach without being considered out of control, while the lower control limit (LCL) is the minimum value. Any data point that falls outside these limits indicates that the process is not in control.
Types of Control Charts
There are several types of control charts, including:
- X-bar chart: used to monitor the average performance of a process
- R-chart: used to monitor the range of a process
- S-chart: used to monitor the standard deviation of a process
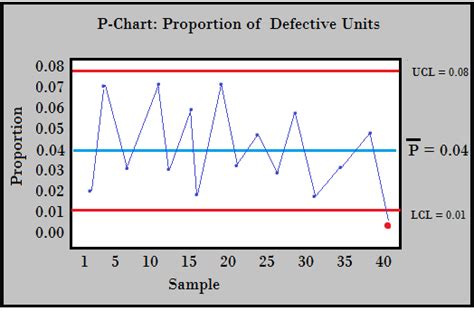
- P-chart: used to monitor the proportion of defective units
- C-chart: used to monitor the count of defective units
Calculating UCL and LCL in Excel
To calculate UCL and LCL in Excel, you need to know the type of control chart you are using and the relevant formulas. Here are the steps to calculate UCL and LCL for an X-bar chart:
- Calculate the average (X-bar) of the data
- Calculate the standard deviation (sigma) of the data
- Determine the number of subgroups (k)
- Determine the subgroup size (n)
- Calculate the UCL and LCL using the following formulas:
UCL = X-bar + (3 * sigma) / sqrt(n) LCL = X-bar - (3 * sigma) / sqrt(n)
You can use the following Excel formulas to calculate UCL and LCL:
- UCL: =AVERAGE(data) + 3*STDEV(data)/SQRT(n)
- LCL: =AVERAGE(data) - 3*STDEV(data)/SQRT(n)
Where data is the range of cells containing the data, n is the subgroup size, and STDEV is the standard deviation of the data.
Example
Suppose we have a set of data representing the average height of a product over time. We want to calculate the UCL and LCL for an X-bar chart.
| Subgroup | Height |
|---|---|
| 1 | 10.2 |
| 2 | 10.5 |
| 3 | 10.1 |
| 4 | 10.3 |
| 5 | 10.4 |
To calculate the UCL and LCL, we first calculate the average and standard deviation of the data.
| Average | Standard Deviation |
|---|---|
| 10.3 | 0.12 |
Next, we determine the subgroup size (n) and the number of subgroups (k).
| Subgroup Size | Number of Subgroups |
|---|---|
| 5 | 5 |
Now, we can calculate the UCL and LCL using the formulas above.
| UCL | LCL |
|---|---|
| 10.6 | 10.0 |
Interpreting UCL and LCL Results
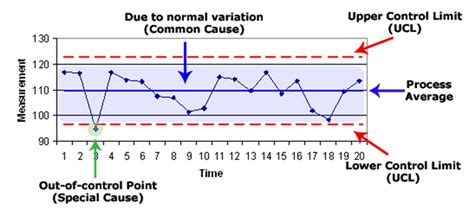
Once you have calculated the UCL and LCL, you can use them to monitor the performance of your process. Any data point that falls outside the UCL or LCL indicates that the process is not in control.
Here are some common interpretations of UCL and LCL results:
- If a data point falls above the UCL, it indicates that the process is producing more than expected.
- If a data point falls below the LCL, it indicates that the process is producing less than expected.
- If a data point falls within the UCL and LCL, it indicates that the process is in control.
Conclusion
Calculating UCL and LCL in Excel is a straightforward process that can help you monitor and control processes in various industries. By understanding the formulas and concepts involved, you can easily calculate UCL and LCL for different types of control charts. Remember to interpret the results correctly to ensure that your process is in control.
Gallery of Control Charts
Control Chart Gallery
