Intro
Unlock the secrets of limit superior and limit inferior, crucial concepts in real analysis. Learn how these mathematical constructs help determine the upper and lower bounds of sequences and functions, and understand their significance in calculus, topology, and mathematical analysis with practical examples and explanations.
The concepts of limit superior and limit inferior are fundamental in mathematics, particularly in real analysis and measure theory. These concepts help us understand the behavior of sequences of sets and their relationships with other mathematical objects. In this article, we will delve into the definitions, properties, and applications of limit superior and limit inferior, providing a comprehensive understanding of these important mathematical concepts.
Understanding Limit Superior and Limit Inferior
To begin with, let's consider a sequence of sets {A_n} in a measurable space (X, Σ, μ). The limit superior of this sequence, denoted by lim sup A_n, is the set of all points that are in infinitely many of the sets A_n. Similarly, the limit inferior of the sequence, denoted by lim inf A_n, is the set of all points that are in all but finitely many of the sets A_n.
Formal Definitions

Formally, the limit superior and limit inferior of a sequence of sets {A_n} are defined as:
lim sup A_n = ∩{n=1}^∞ ∪{k=n}^∞ A_k
lim inf A_n = ∪{n=1}^∞ ∩{k=n}^∞ A_k
Properties of Limit Superior and Limit Inferior
The limit superior and limit inferior of a sequence of sets have several important properties. For instance, the limit superior of a sequence of sets is always a superset of the limit inferior. Additionally, the limit superior and limit inferior of a sequence of sets are both monotone with respect to the sequence.
Monotonicity of Limit Superior and Limit Inferior
If {A_n} is a sequence of sets such that A_n ⊆ A_{n+1} for all n, then:
lim sup A_n ⊆ lim sup A_{n+1}
lim inf A_n ⊆ lim inf A_{n+1}
Applications of Limit Superior and Limit Inferior
The concepts of limit superior and limit inferior have numerous applications in mathematics and other fields. For example, in probability theory, the limit superior and limit inferior of a sequence of events are used to define the notions of almost sure convergence and convergence in probability.
Almost Sure Convergence

A sequence of random variables {X_n} is said to converge almost surely to a random variable X if:
P(lim sup {|X_n - X| > ε}) = 0
for all ε > 0.
Relationship with Other Mathematical Concepts
The limit superior and limit inferior are closely related to other mathematical concepts, such as the concept of a limit point. In fact, the limit superior of a sequence of sets is precisely the set of all limit points of the sequence.
Limit Points

A point x is said to be a limit point of a sequence of sets {A_n} if:
x ∈ lim sup A_n
Gallery of Limit Superior and Limit Inferior
Limit Superior and Limit Inferior Image Gallery
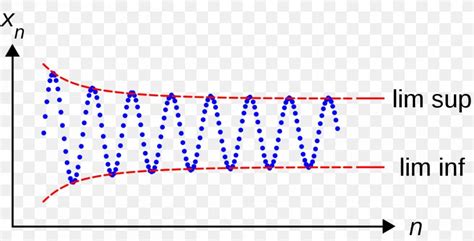
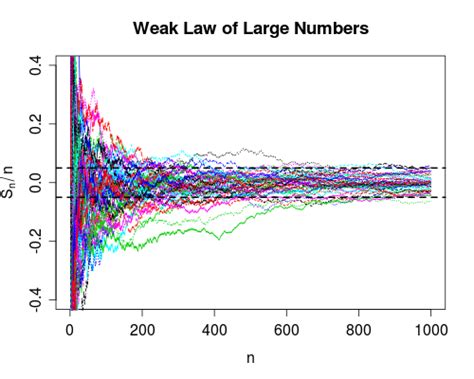



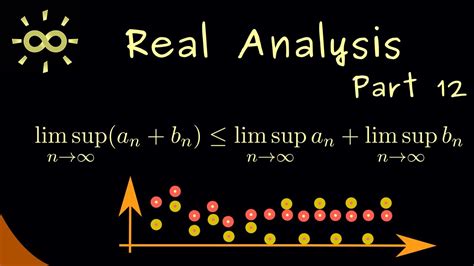



In conclusion, the limit superior and limit inferior are important mathematical concepts that help us understand the behavior of sequences of sets. These concepts have numerous applications in mathematics and other fields, and are closely related to other mathematical concepts, such as the concept of a limit point. We hope this article has provided a comprehensive understanding of the limit superior and limit inferior, and has inspired readers to explore these concepts further.
Share Your Thoughts
We invite readers to share their thoughts and comments on this article. Have you encountered the limit superior and limit inferior in your mathematical journey? How have you applied these concepts in your work or studies? Share your experiences and insights with us, and let's continue the conversation.
