Intro
Discover the fascinating world of geometry with our in-depth explanation of the 5 lines of symmetry on a pentagon. Learn about reflection symmetry, rotational symmetry, and the unique properties of pentagons. Explore the concepts of line symmetry, axis of symmetry, and symmetry in geometry. Perfect for math students and enthusiasts alike!
Symmetry is a fundamental concept in geometry and art, referring to the quality of being unchanged under a particular transformation, such as reflection or rotation. One of the most interesting and complex shapes in geometry is the pentagon, a five-sided polygon with a rich history and numerous applications. In this article, we will delve into the world of pentagons and explore the concept of lines of symmetry, particularly the five lines of symmetry that can be found in a regular pentagon.
Lines of symmetry are imaginary lines that divide a shape into two identical halves, creating a mirror image on either side of the line. In the case of a regular pentagon, there are five lines of symmetry that can be drawn, each passing through a vertex and the midpoint of the opposite side. These lines of symmetry play a crucial role in understanding the geometric properties of the pentagon and have numerous applications in art, architecture, and design.
Understanding the concept of lines of symmetry is essential for various mathematical and artistic endeavors, from creating intricate patterns and designs to solving complex problems in geometry and engineering. By exploring the five lines of symmetry on a pentagon, we can gain a deeper understanding of the underlying principles of geometry and develop our problem-solving skills.
What are Lines of Symmetry?
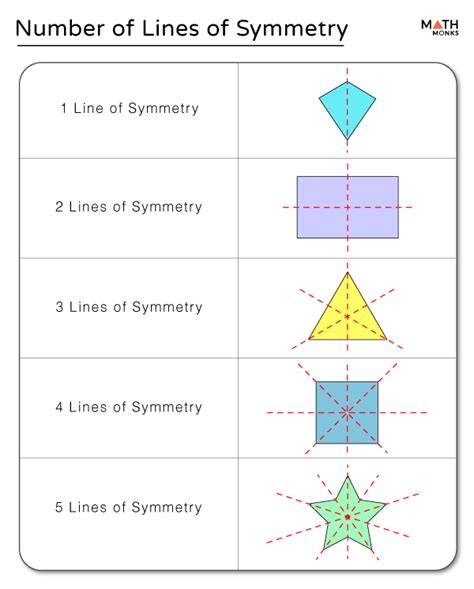
Lines of symmetry are imaginary lines that divide a shape into two identical halves, creating a mirror image on either side of the line. These lines can be drawn in various directions, depending on the shape and its properties. In the case of a regular pentagon, the lines of symmetry pass through the vertices and the midpoints of the opposite sides.
There are different types of lines of symmetry, including:
- Line of Reflection: A line that divides a shape into two identical halves, creating a mirror image on either side.
- Line of Rotation: A line that divides a shape into two identical halves, creating a rotational symmetry.
- Line of Translation: A line that divides a shape into two identical halves, creating a translational symmetry.
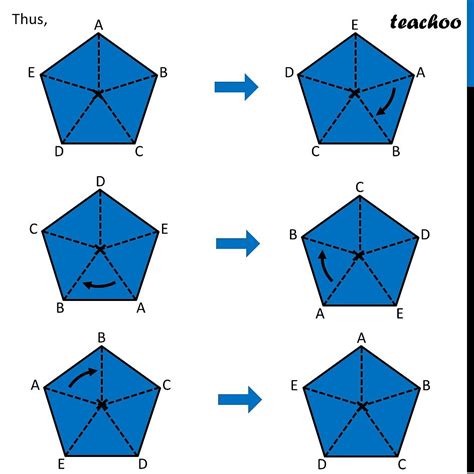
Types of Symmetry
Symmetry can be classified into different types, including:
- Reflection Symmetry: A shape has reflection symmetry if it can be divided into two identical halves by a line of reflection.
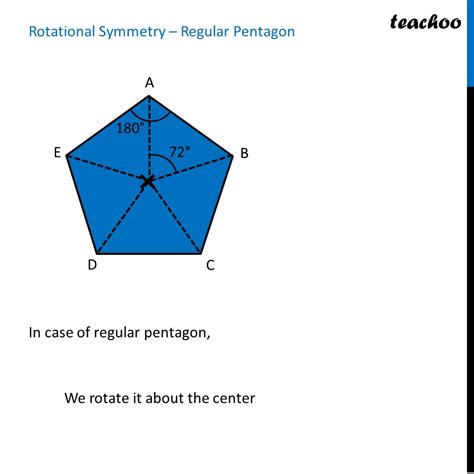
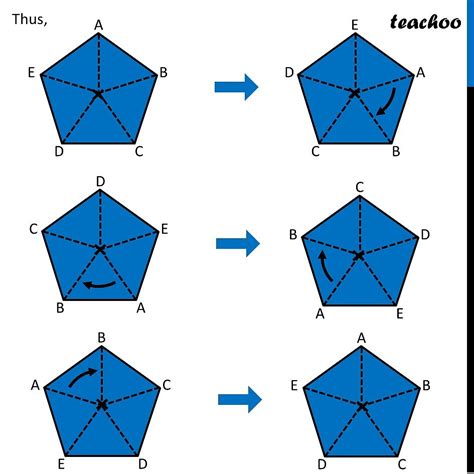
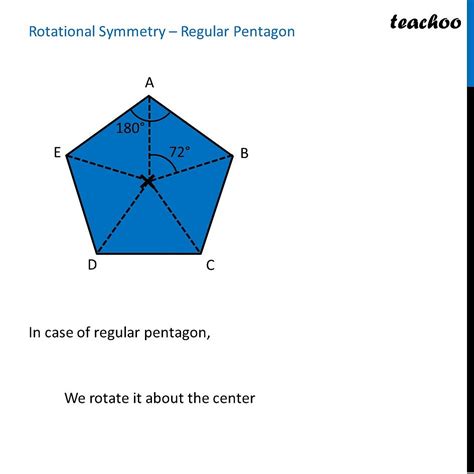
- Rotational Symmetry: A shape has rotational symmetry if it can be rotated around a central point to create an identical image.
- Translational Symmetry: A shape has translational symmetry if it can be translated (moved) to create an identical image.
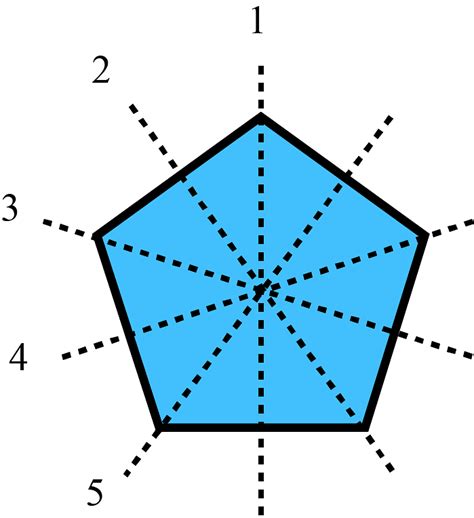
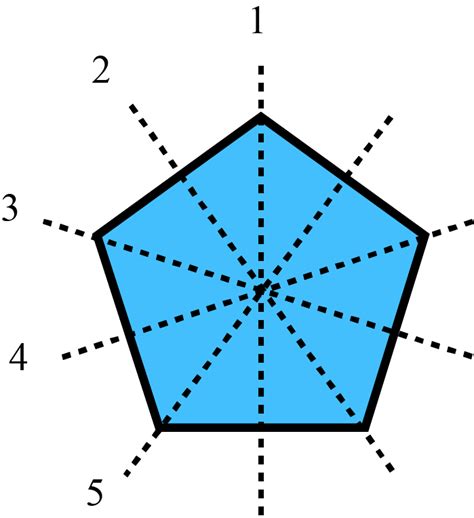
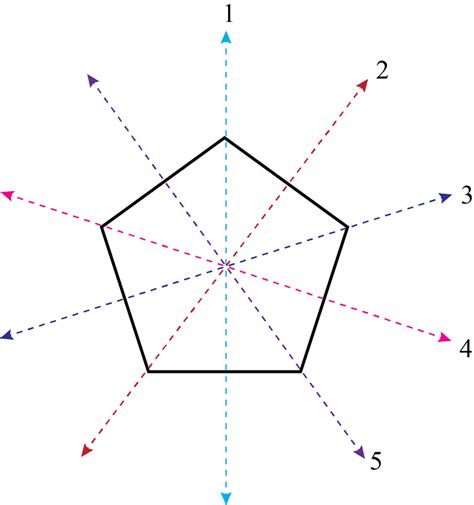
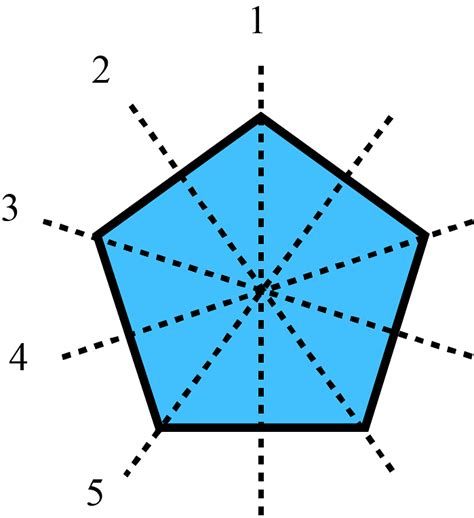
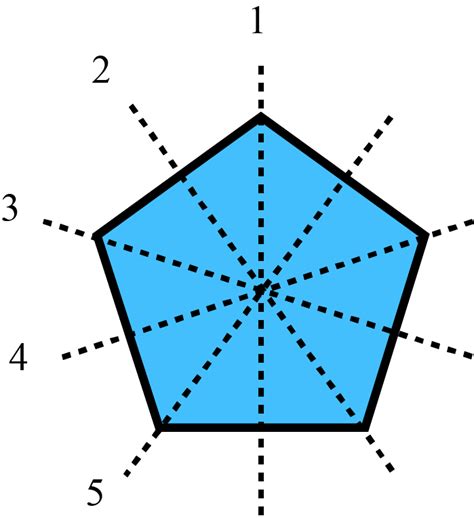
The Five Lines of Symmetry on a Pentagon
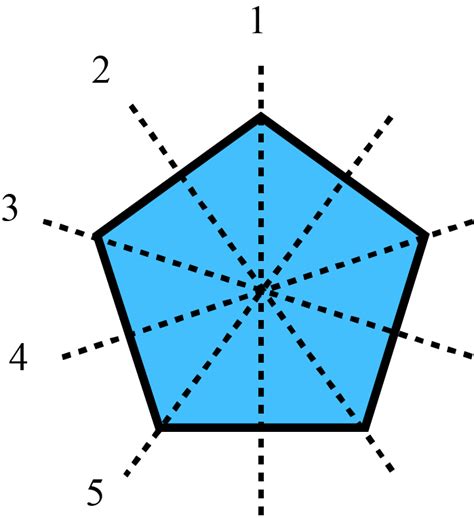
A regular pentagon has five lines of symmetry, each passing through a vertex and the midpoint of the opposite side. These lines of symmetry play a crucial role in understanding the geometric properties of the pentagon and have numerous applications in art, architecture, and design.
The five lines of symmetry on a pentagon can be drawn as follows:
- Line 1: Passes through vertex A and the midpoint of side BC.
- Line 2: Passes through vertex B and the midpoint of side CD.
- Line 3: Passes through vertex C and the midpoint of side DE.
- Line 4: Passes through vertex D and the midpoint of side EA.
- Line 5: Passes through vertex E and the midpoint of side AB.
Properties of the Lines of Symmetry
The lines of symmetry on a pentagon have several important properties, including:
- Perpendicularity: Each line of symmetry is perpendicular to the side it intersects.
- Bisecting: Each line of symmetry bisects the angle at the vertex it passes through.
- Intersection: The lines of symmetry intersect at a single point, called the center of the pentagon.
Applications of the Lines of Symmetry
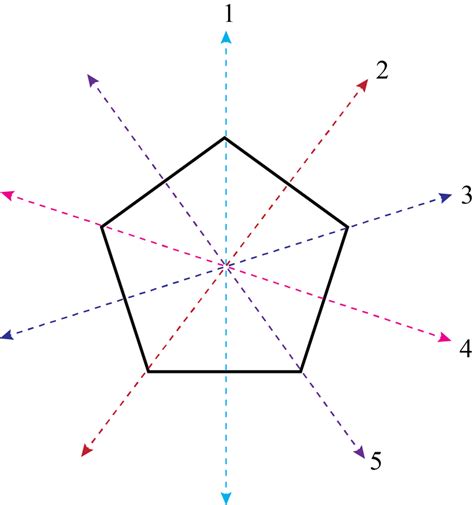
The lines of symmetry on a pentagon have numerous applications in art, architecture, and design. Some examples include:
- Tessellations: The lines of symmetry can be used to create intricate tessellations and patterns.
- Mosaics: The lines of symmetry can be used to create beautiful mosaics and designs.
- Architecture: The lines of symmetry can be used in the design of buildings and structures to create a sense of balance and harmony.
Conclusion
In conclusion, the five lines of symmetry on a pentagon are a fundamental concept in geometry and have numerous applications in art, architecture, and design. By understanding the properties and applications of these lines, we can gain a deeper appreciation for the beauty and complexity of geometry.
Gallery of Pentagon Symmetry
Pentagon Symmetry Image Gallery
We hope this article has provided a comprehensive understanding of the five lines of symmetry on a pentagon. If you have any questions or comments, please feel free to share them with us.
