Intro
Boost your data analysis skills with our expert guide on calculating margin of error in Excel. Learn 5 easy methods to determine sample size, confidence intervals, and error margins using formulas and charts. Master statistical analysis and make informed decisions with our step-by-step tutorial on margin of error calculation.
Calculating the margin of error in Excel can be a daunting task, especially for those without a background in statistics. However, it's an essential step in understanding the accuracy of your data and making informed decisions. In this article, we'll explore five ways to calculate the margin of error in Excel, using different formulas and techniques.
Why is Margin of Error Important?
Before we dive into the calculations, let's quickly discuss why margin of error is important. The margin of error, also known as the confidence interval, is a statistical measure that indicates the amount of uncertainty associated with a sample's estimate of a population parameter. In other words, it tells you how accurate your sample data is likely to be.
Having a small margin of error is crucial in many fields, such as business, medicine, and social sciences, where accurate predictions and decisions are critical. A large margin of error can lead to incorrect conclusions and poor decision-making.
Method 1: Using the CONFIDENCE Function
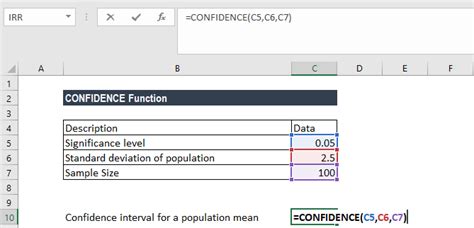
The CONFIDENCE function in Excel is a simple and straightforward way to calculate the margin of error. This function returns the margin of error for a given confidence level and sample size.
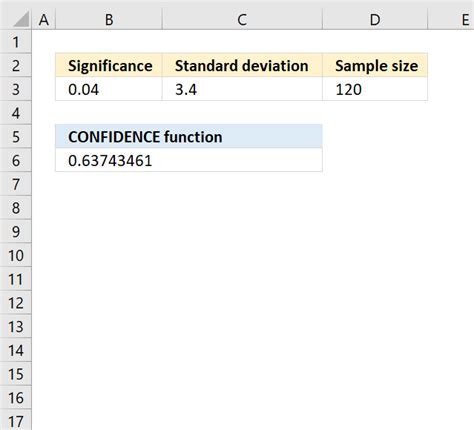
The syntax for the CONFIDENCE function is:
CONFIDENCE(alpha, standard_dev, size)
Where:
- alpha is the desired confidence level (e.g., 0.05 for 95% confidence)
- standard_dev is the standard deviation of the population
- size is the sample size
For example, if you want to calculate the margin of error for a sample of 100 data points with a standard deviation of 10, using a 95% confidence level, you would use the following formula:
=CONFIDENCE(0.05, 10, 100)
Method 2: Using the NORMSINV Function
The NORMSINV function in Excel is another way to calculate the margin of error. This function returns the z-score corresponding to a given probability.
The syntax for the NORMSINV function is:
NORMSINV(probability)
Where:
- probability is the desired confidence level (e.g., 0.95 for 95% confidence)
To calculate the margin of error using the NORMSINV function, you would use the following formula:
=(standard_dev / sqrt(size)) * NORMSINV(1 - (alpha / 2))
Where:
- standard_dev is the standard deviation of the population
- size is the sample size
- alpha is the desired confidence level (e.g., 0.05 for 95% confidence)
For example, if you want to calculate the margin of error for a sample of 100 data points with a standard deviation of 10, using a 95% confidence level, you would use the following formula:
=(10 / sqrt(100)) * NORMSINV(1 - (0.05 / 2))
Method 3: Using the TINV Function
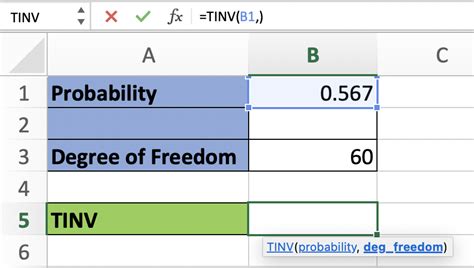
The TINV function in Excel is a more advanced way to calculate the margin of error, especially when dealing with small sample sizes.
The syntax for the TINV function is:
TINV(probability, degrees_freedom)
Where:
- probability is the desired confidence level (e.g., 0.95 for 95% confidence)
- degrees_freedom is the number of degrees of freedom (n-1)
To calculate the margin of error using the TINV function, you would use the following formula:
=(standard_dev / sqrt(size)) * TINV(1 - (alpha / 2), size - 1)
Where:
- standard_dev is the standard deviation of the population
- size is the sample size
- alpha is the desired confidence level (e.g., 0.05 for 95% confidence)
For example, if you want to calculate the margin of error for a sample of 20 data points with a standard deviation of 10, using a 95% confidence level, you would use the following formula:
=(10 / sqrt(20)) * TINV(1 - (0.05 / 2), 20 - 1)
Method 4: Using the Z-Test
The Z-test is a statistical test used to determine whether a sample mean is significantly different from a known population mean.
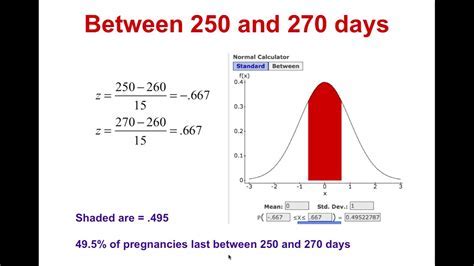
To calculate the margin of error using the Z-test, you would use the following formula:
=(sample_mean - population_mean) / (standard_dev / sqrt(size))
Where:
- sample_mean is the sample mean
- population_mean is the known population mean
- standard_dev is the standard deviation of the population
- size is the sample size
For example, if you want to calculate the margin of error for a sample of 100 data points with a sample mean of 50, a population mean of 40, and a standard deviation of 10, you would use the following formula:
=(50 - 40) / (10 / sqrt(100))
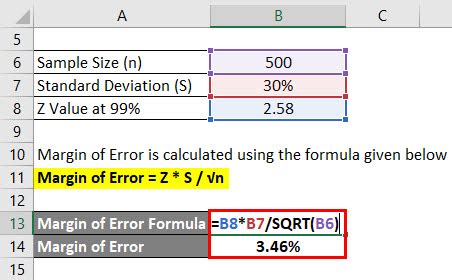
Method 5: Using the Confidence Interval Formula
The confidence interval formula is a more general way to calculate the margin of error.

The formula is:
margin_of_error = (z-score * standard_dev) / sqrt(size)
Where:
- z-score is the z-score corresponding to the desired confidence level
- standard_dev is the standard deviation of the population
- size is the sample size
For example, if you want to calculate the margin of error for a sample of 100 data points with a standard deviation of 10, using a 95% confidence level, you would use the following formula:
=(1.96 * 10) / sqrt(100)
Gallery of Margin of Error Formulas
Margin of Error Formulas
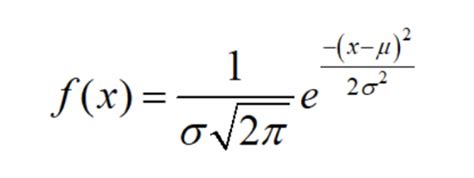
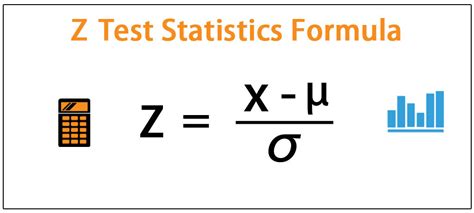



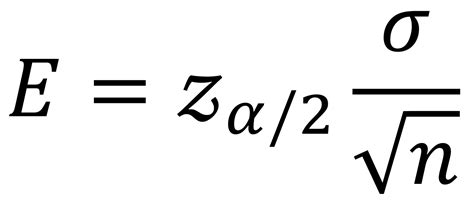

Conclusion
Calculating the margin of error in Excel can be a complex task, but by using the right formulas and techniques, you can ensure accurate results. Whether you use the CONFIDENCE function, NORMSINV function, TINV function, Z-test, or confidence interval formula, it's essential to understand the underlying statistics and assumptions. By mastering these methods, you'll be able to make informed decisions and take your data analysis to the next level.
We hope this article has helped you understand the different ways to calculate the margin of error in Excel. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences in the comments below!
