Algebra Cheat Sheet: Quick Reference Guide

Algebra is a fundamental subject that can be challenging for many students. With so many formulas, equations, and rules to remember, it's easy to get overwhelmed. That's where an algebra cheat sheet comes in handy. In this article, we'll provide a comprehensive quick reference guide to help you navigate the world of algebra.

Whether you're a student struggling to keep up with your algebra coursework or a professional looking to brush up on your math skills, this cheat sheet will cover all the essential concepts and formulas you need to know. From basic equations to advanced functions, we'll break down the key concepts into easy-to-understand sections.

So, let's dive in and explore the world of algebra!

Algebra Basics

Before we dive into the more advanced topics, let's review the basics of algebra. Algebra is a branch of mathematics that deals with the study of variables and their relationships. It involves the use of symbols, equations, and formulas to solve problems.

Here are some key concepts to remember:

• Variables: Letters or symbols that represent unknown values.
• Constants: Numbers that do not change value.
• Coefficients: Numbers that multiply variables.
• Terms: Parts of an expression separated by addition or subtraction.

Equations and Formulas

Equations are statements that express the equality of two expressions. Formulas are equations that describe a specific relationship between variables.

Here are some key equations and formulas to remember:

• Linear Equations: Equations in the form of ax + b = c, where a, b, and c are constants.
• Quadratic Equations: Equations in the form of ax^2 + bx + c = 0, where a, b, and c are constants.
• Exponential Equations: Equations in the form of a^x = b, where a and b are constants.
• Logarithmic Equations: Equations in the form of log(a) = b, where a and b are constants.

Functions

Functions are relationships between variables that assign each input to exactly one output.

Here are some key concepts to remember:

• Domain: The set of all possible input values.
• Range: The set of all possible output values.
• Linear Functions: Functions in the form of f(x) = ax + b, where a and b are constants.
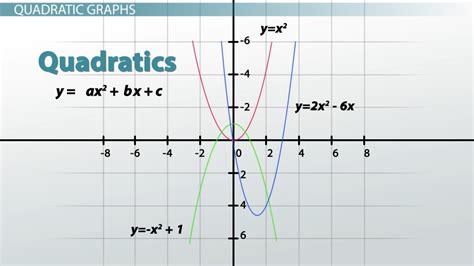
• Quadratic Functions: Functions in the form of f(x) = ax^2 + bx + c, where a, b, and c are constants.

Graphing

Graphing is a way of visualizing relationships between variables.

Here are some key concepts to remember:

• X-Axis: The horizontal axis that represents the input values.
• Y-Axis: The vertical axis that represents the output values.
• Graph: A visual representation of the relationship between variables.

Inequalities

Inequalities are statements that express the relationship between two expressions.

Here are some key concepts to remember:

• Less Than: <
• Greater Than: >
• Less Than or Equal To: ≤
• Greater Than or Equal To: ≥

Systems of Equations

Systems of equations are sets of two or more equations that must be solved simultaneously.

Here are some key concepts to remember:

• Substitution Method: A method that involves solving one equation for one variable and substituting that expression into the other equation.
• Elimination Method: A method that involves adding or subtracting equations to eliminate one variable.

Sequences and Series

Sequences and series are used to study patterns and relationships between numbers.

Here are some key concepts to remember:

• Sequence: A list of numbers in a specific order.
• Series: The sum of a sequence.
• Arithmetic Sequence: A sequence in which each term is obtained by adding a fixed constant to the previous term.
• Geometric Sequence: A sequence in which each term is obtained by multiplying the previous term by a fixed constant.

Mathematical Induction

Mathematical induction is a method used to prove the validity of a statement for all positive integers.

Here are some key concepts to remember:

• Base Case: The first case to be proven.
• Inductive Step: The step that involves assuming the statement is true for one positive integer and proving it is true for the next positive integer.

Algebra Image Gallery

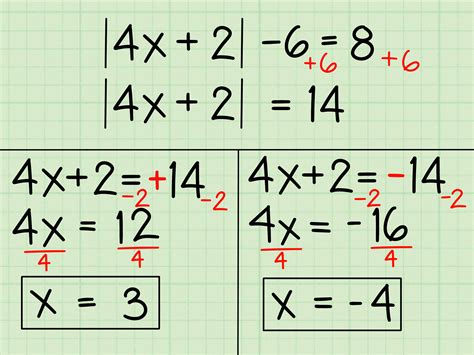
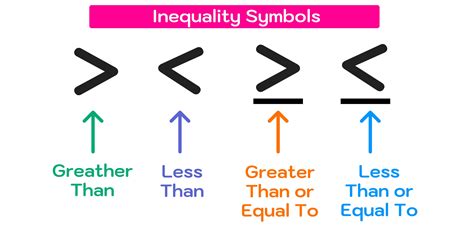
We hope this comprehensive algebra cheat sheet has been helpful in your studies. Remember, practice makes perfect, so be sure to work through plenty of examples and exercises to reinforce your understanding of these concepts. If you have any questions or need further clarification on any of the topics covered, feel free to ask in the comments below. Happy learning!