Master The S Curve In Excel With 5 Essential Formulas

The S Curve, also known as the Sigmoid Curve or Logistic Curve, is a fundamental concept in data analysis and visualization. It's a mathematical model that describes how things grow, peak, and then decline. In this article, we'll explore the importance of the S Curve in Excel and delve into the 5 essential formulas you need to master it.

Whether you're a data analyst, financial modeler, or simply a curious individual, understanding the S Curve can help you make sense of complex data and uncover hidden patterns. With the right tools and techniques, you can unlock new insights and make more informed decisions.

What is the S Curve?

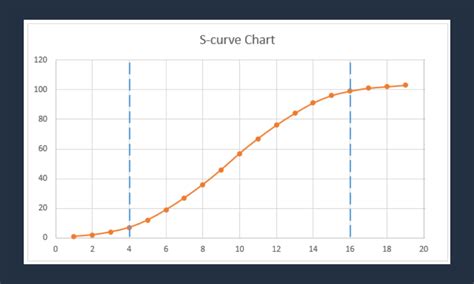
The S Curve is a mathematical function that describes how a quantity changes over time, often in a non-linear fashion. It's characterized by an initial slow growth phase, followed by rapid acceleration, and finally, a plateau or decline. This curve is commonly observed in various domains, including population growth, product adoption, and even social media trends.

Why is the S Curve important in Excel?

The S Curve has numerous practical applications in Excel, particularly in data analysis, forecasting, and modeling. By mastering the S Curve, you can:

• Create more accurate forecasts and predictions
• Analyze and understand complex data patterns
• Visualize and communicate insights more effectively
• Make informed decisions based on data-driven insights

Formula 1: The Logistic Function

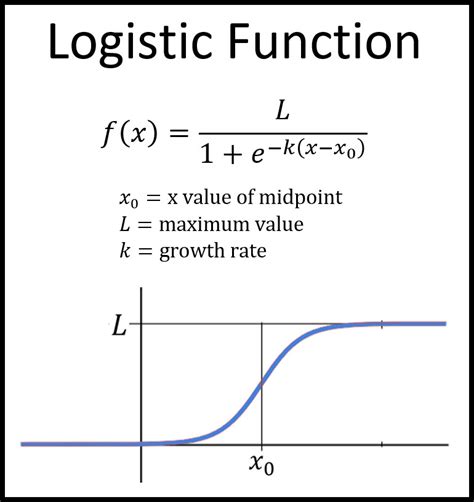
The Logistic Function is the foundation of the S Curve. It's a mathematical formula that describes the S-shaped curve:

y = 1 / (1 + e^(-x))

Where:

• y is the output value (between 0 and 1)
• e is the base of the natural logarithm (approximately 2.718)
• x is the input value

This formula is the building block for more complex S Curve calculations.

Formula 2: The S Curve Formula

The S Curve Formula is a variation of the Logistic Function, which allows you to calculate growth rates:

y = (1 / (1 + e^(-(x - c) / b))) * d

Where:

• y is the output value
• e is the base of the natural logarithm (approximately 2.718)
• x is the input value
• c is the inflection point (where the curve changes direction)
• b is the growth rate
• d is the maximum value (the plateau)

This formula is useful for modeling growth rates and forecasting future values.

Formula 3: The Hill Equation

The Hill Equation is a variant of the S Curve Formula, which is commonly used in biochemistry and pharmacology to model cooperative binding:

y = (x^n / (Kd + x^n))

Where:

• y is the output value
• x is the input value
• n is the Hill coefficient (describes the cooperativity of binding)
• Kd is the dissociation constant (describes the binding affinity)

This formula is useful for modeling complex binding interactions.

Formula 4: The Gompertz Curve

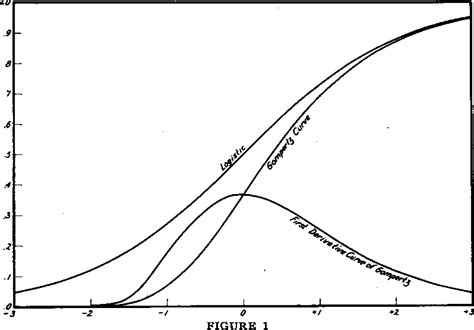
The Gompertz Curve is another type of S Curve, which is commonly used to model population growth and disease progression:

y = a * e^(-e^(-b * x))

Where:

• y is the output value
• a is the maximum value (the plateau)
• b is the growth rate
• x is the input value

This formula is useful for modeling population dynamics and disease progression.

Formula 5: The Weibull Distribution

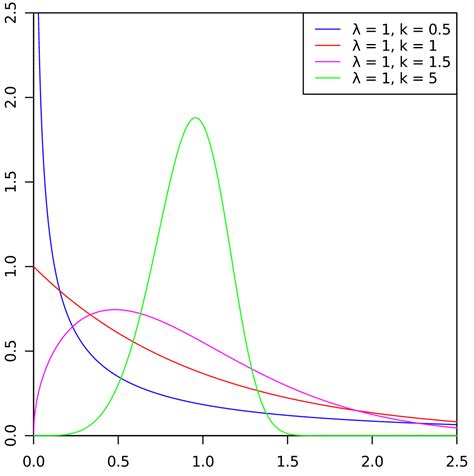
The Weibull Distribution is a probability distribution that is commonly used to model failure rates and reliability:

f(x) = (k / λ) * (x / λ)^(k-1) * e^(-(x/λ)^k)

Where:

• f(x) is the probability density function
• k is the shape parameter (describes the failure rate)
• λ is the scale parameter (describes the reliability)

This formula is useful for modeling failure rates and reliability.

S Curve Gallery

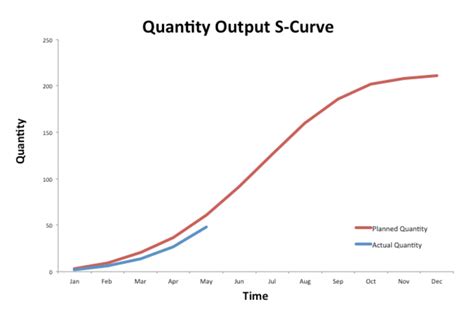
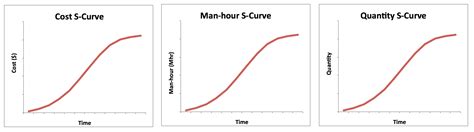
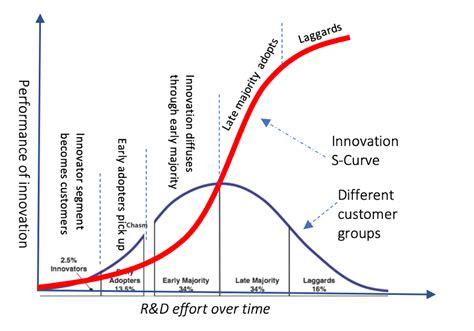
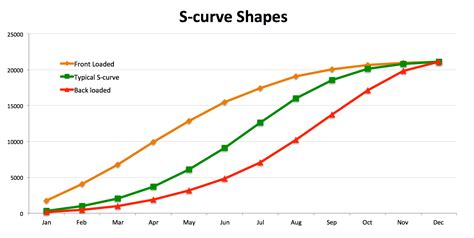
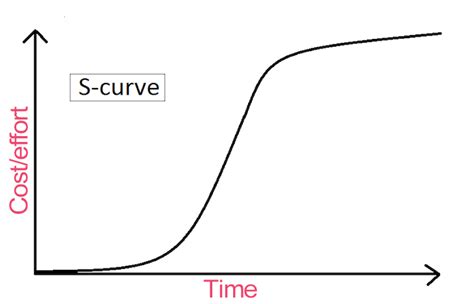
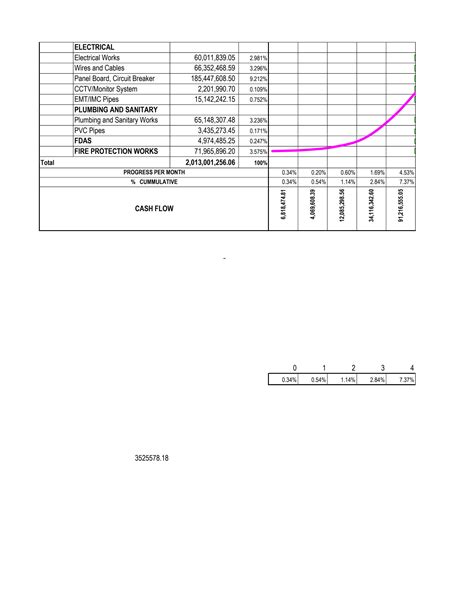
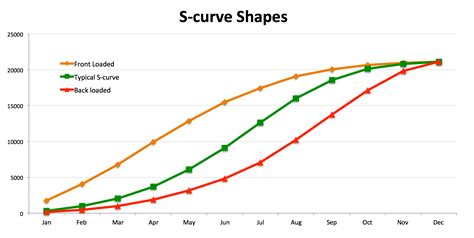
In conclusion, mastering the S Curve in Excel requires a solid understanding of the underlying mathematical formulas. By mastering these 5 essential formulas, you'll be able to analyze and model complex data patterns, make more accurate forecasts, and communicate insights more effectively. Take your Excel skills to the next level and unlock new insights with the S Curve. Share your experiences and questions in the comments below!