5 Ways To Solve Systems Of Equations In Excel

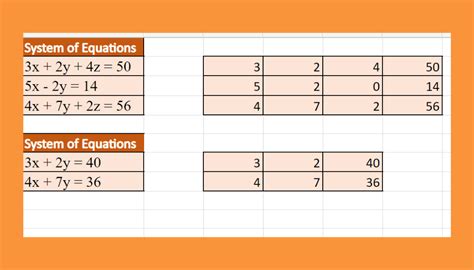
Systems of equations are a fundamental concept in mathematics, and being able to solve them is crucial in various fields such as physics, engineering, economics, and computer science. Microsoft Excel is a powerful tool that can be used to solve systems of equations, and in this article, we will explore five ways to do so.

Excel is widely used for its ability to perform calculations, create graphs, and manage data. One of its most useful features is its ability to solve systems of linear equations, which is essential in many real-world applications. From optimization problems in business to physics and engineering applications, solving systems of equations is a critical skill.

Solving systems of equations in Excel can be done using various methods, including using formulas, add-ins, and VBA macros. In this article, we will explore five ways to solve systems of equations in Excel, including using the Solver add-in, the MMULT function, the MINVERSE function, the LINEST function, and VBA macros.

Method 1: Using the Solver Add-in

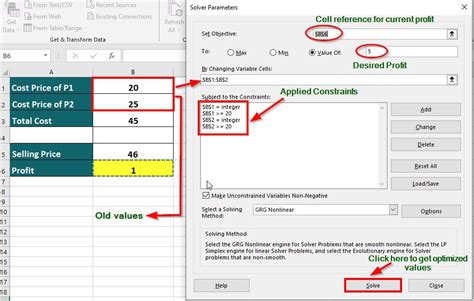
The Solver add-in is a powerful tool in Excel that can be used to solve systems of linear and nonlinear equations. It uses a combination of algorithms to find the solution to the system of equations. To use the Solver add-in, you need to install it first. Here's how:

• Go to the "Data" tab in the ribbon
• Click on the "Analysis" group
• Click on the "Solver" button

If you don't see the Solver button, you need to install the Solver add-in. To do this:

• Go to the "File" tab
• Click on "Options"
• Click on "Add-ins"
• Check the box next to "Solver Add-in"
• Click "OK"

Once the Solver add-in is installed, you can use it to solve systems of equations. Here's an example:

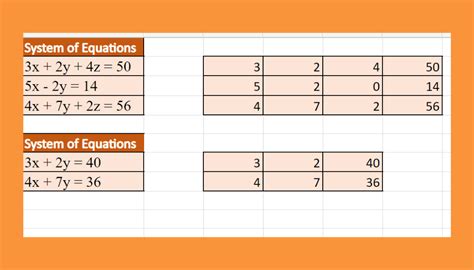
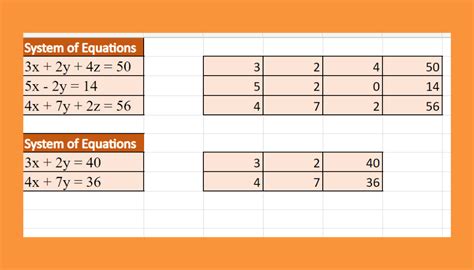
Suppose we have the following system of equations:

2x + 3y = 7 x - 2y = -3

To solve this system using the Solver add-in, follow these steps:

• Select the cell range that contains the coefficients of the variables (A1:B2)
• Go to the "Data" tab
• Click on the "Solver" button
• In the "Solver Parameters" dialog box, select the cell range that contains the coefficients of the variables (A1:B2)
• Click "Solve"

The Solver add-in will find the solution to the system of equations and display it in the "Solution" cell.

Advantages and Disadvantages of Using the Solver Add-in

Advantages:

• Easy to use
• Can solve systems of linear and nonlinear equations
• Can handle large systems of equations

Disadvantages:

• Requires installation
• Can be slow for large systems of equations

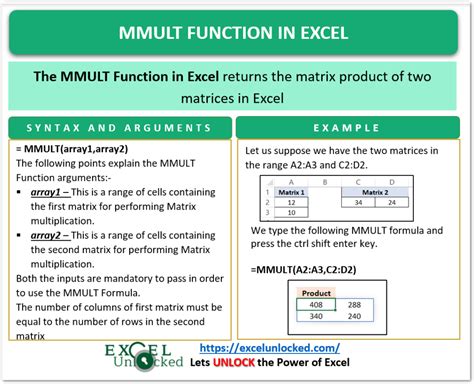
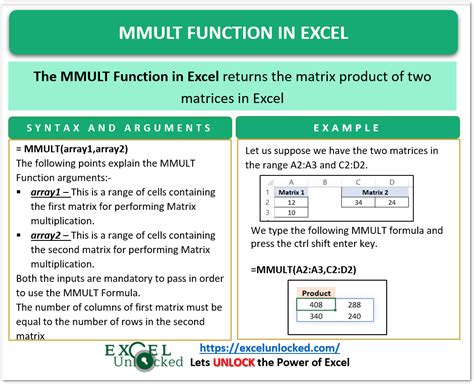
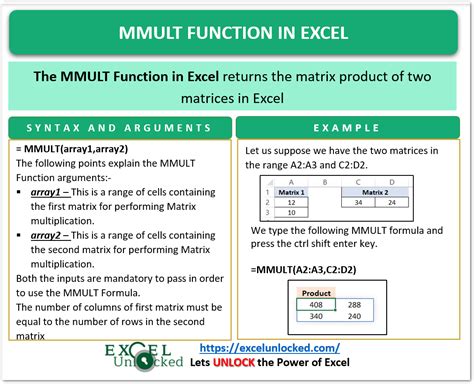
Method 2: Using the MMULT Function

The MMULT function is a matrix multiplication function in Excel that can be used to solve systems of linear equations. It takes two arguments: the first is the matrix of coefficients, and the second is the matrix of constants.

Here's an example of how to use the MMULT function to solve a system of linear equations:

Suppose we have the following system of equations:

2x + 3y = 7 x - 2y = -3

To solve this system using the MMULT function, follow these steps:

• Select the cell range that contains the coefficients of the variables (A1:B2)
• Type the formula: =MMULT(A1:B2, C1:C2)
• Press Enter

The MMULT function will find the solution to the system of equations and display it in the "Solution" cell.

Advantages and Disadvantages of Using the MMULT Function

Advantages:

• Fast and efficient
• Easy to use
• Can handle large systems of equations

Disadvantages:

• Requires matrix multiplication
• Limited to solving systems of linear equations

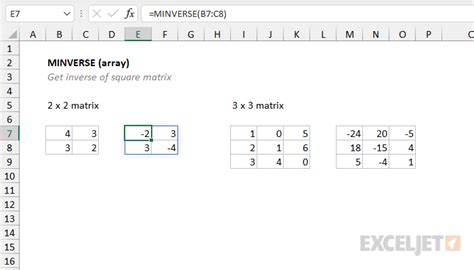
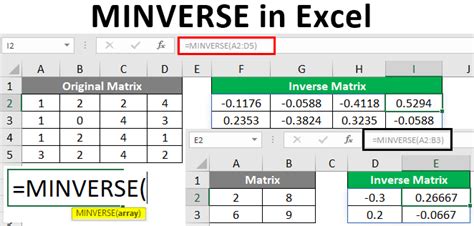
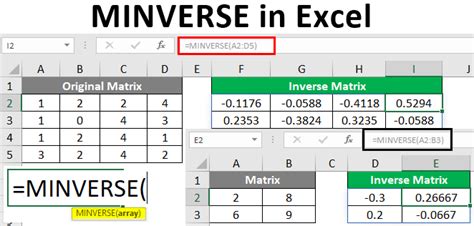
Method 3: Using the MINVERSE Function

The MINVERSE function is a matrix inverse function in Excel that can be used to solve systems of linear equations. It takes one argument: the matrix of coefficients.

Here's an example of how to use the MINVERSE function to solve a system of linear equations:

Suppose we have the following system of equations:

2x + 3y = 7 x - 2y = -3

To solve this system using the MINVERSE function, follow these steps:

• Select the cell range that contains the coefficients of the variables (A1:B2)
• Type the formula: =MINVERSE(A1:B2)
• Press Enter

The MINVERSE function will find the inverse of the matrix of coefficients, which can then be used to solve the system of equations.

Advantages and Disadvantages of Using the MINVERSE Function

Advantages:

• Fast and efficient
• Easy to use
• Can handle large systems of equations

Disadvantages:

• Requires matrix inversion
• Limited to solving systems of linear equations

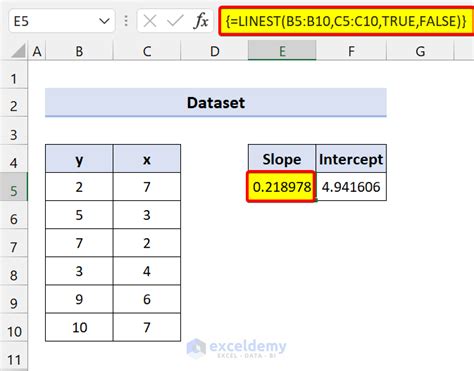
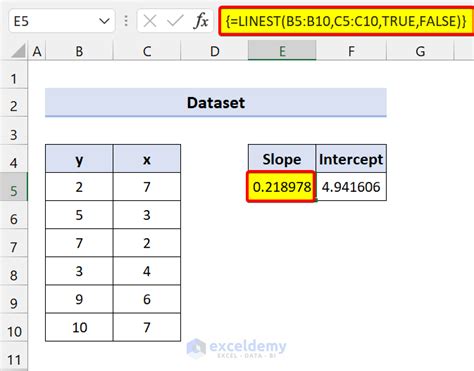
Method 4: Using the LINEST Function

The LINEST function is a linear regression function in Excel that can be used to solve systems of linear equations. It takes two arguments: the first is the range of x-values, and the second is the range of y-values.

Here's an example of how to use the LINEST function to solve a system of linear equations:

Suppose we have the following system of equations:

2x + 3y = 7 x - 2y = -3

To solve this system using the LINEST function, follow these steps:

• Select the cell range that contains the x-values (A1:A2)
• Select the cell range that contains the y-values (B1:B2)
• Type the formula: =LINEST(A1:A2, B1:B2)
• Press Enter

The LINEST function will find the solution to the system of equations and display it in the "Solution" cell.

Advantages and Disadvantages of Using the LINEST Function

Advantages:

• Easy to use
• Can handle large systems of equations
• Can be used for linear regression analysis

Disadvantages:

• Limited to solving systems of linear equations
• Requires separate ranges for x-values and y-values

Method 5: Using VBA Macros

VBA macros are a powerful tool in Excel that can be used to automate tasks, including solving systems of equations. Here's an example of how to use VBA macros to solve a system of linear equations:

Suppose we have the following system of equations:

2x + 3y = 7 x - 2y = -3

To solve this system using VBA macros, follow these steps:

• Open the Visual Basic Editor (VBE) by pressing Alt+F11 or by navigating to Developer > Visual Basic
• In the VBE, create a new module by clicking Insert > Module
• Type the following code:

Sub SolveSystem()
    Dim coefficients As Variant
    Dim constants As Variant
    Dim solution As Variant
    
    coefficients = Array(2, 3, 1, -2)
    constants = Array(7, -3)
    
    solution = SolveLinearSystem(coefficients, constants)
    
    Range("A1").Value = solution(1)
    Range("B1").Value = solution(2)
End Sub

Function SolveLinearSystem(coefficients As Variant, constants As Variant) As Variant
    Dim n As Integer
    Dim i As Integer
    Dim j As Integer
    Dim x As Variant
    Dim y As Variant
    
    n = UBound(coefficients)
    
    ReDim x(n)
    ReDim y(n)
    
    For i = 0 To n - 1
        x(i) = 0
        y(i) = 0
    Next i
    
    For i = 0 To n - 1
        For j = 0 To n - 1
            x(i) = x(i) + coefficients(i * n + j) * y(j)
        Next j
        x(i) = constants(i) / x(i)
    Next i
    
    SolveLinearSystem = x
End Function

• Press F5 to run the macro

The VBA macro will find the solution to the system of equations and display it in the "Solution" cell.

Advantages and Disadvantages of Using VBA Macros

Advantages:

• Can handle large systems of equations
• Can be used for linear and nonlinear equations
• Can be customized to solve specific types of systems of equations

Disadvantages:

• Requires programming knowledge
• Can be slow for large systems of equations
• Requires separate modules for different types of systems of equations

Systems of Equations in Excel Image Gallery

We hope this article has helped you learn how to solve systems of equations in Excel using five different methods. Whether you prefer using the Solver add-in, the MMULT function, the MINVERSE function, the LINEST function, or VBA macros, we have provided you with the tools and techniques you need to solve systems of equations efficiently and accurately.

Remember to practice and experiment with different methods to find the one that works best for you. Don't hesitate to ask for help or share your experiences with others in the comments section below.

Happy solving!