Black Scholes Model In Excel: A Step-By-Step Guide

The Black-Scholes model is a widely used financial model that estimates the value of a call option or a put option. Developed by Fischer Black, Myron Scholes, and Robert Merton in the 1970s, the model has become a cornerstone of modern finance. In this article, we will explore how to implement the Black-Scholes model in Excel, a popular spreadsheet software.

The Black-Scholes model is a complex mathematical formula that requires several inputs, including the current stock price, strike price, time to expiration, risk-free interest rate, and volatility. By using Excel, we can simplify the calculation process and make it more accessible to a wider audience.

Understanding the Black-Scholes Model

The Black-Scholes model is based on the following assumptions:

The stock price follows a geometric Brownian motion
The risk-free interest rate is constant
The volatility of the stock price is constant
The option can only be exercised at expiration

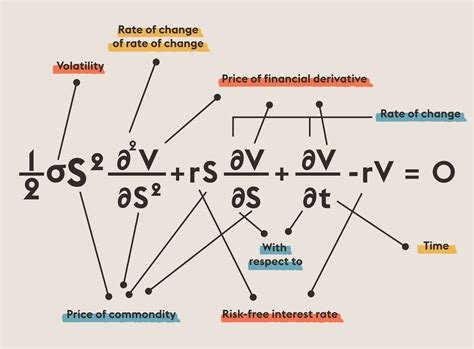
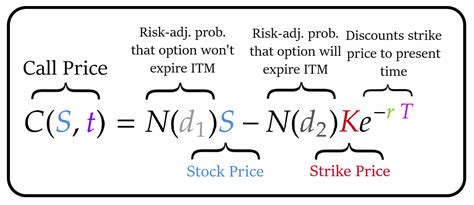
The model estimates the value of a call option or a put option using the following formulas:

Call Option: C = S * N(d1) - X * e^(-rT) * N(d2)

Put Option: P = X * e^(-rT) * N(-d2) - S * N(-d1)

Where:

C is the value of the call option
P is the value of the put option
S is the current stock price
X is the strike price
r is the risk-free interest rate
T is the time to expiration
N(d1) and N(d2) are the cumulative distribution functions of the standard normal distribution
d1 and d2 are the intermediate variables

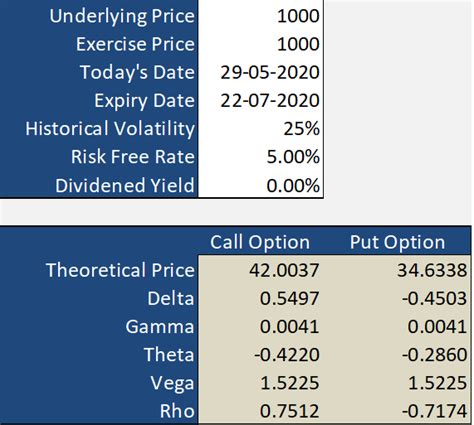
Implementing the Black-Scholes Model in Excel

To implement the Black-Scholes model in Excel, we need to create a spreadsheet that takes the inputs and calculates the outputs. Here's a step-by-step guide:

Create a new spreadsheet in Excel
Create the following input cells:
- Current Stock Price (S)
- Strike Price (X)
- Time to Expiration (T)
- Risk-Free Interest Rate (r)
- Volatility (σ)
Create the following output cells:
- Call Option Value (C)
- Put Option Value (P)
Create the following intermediate cells:
- d1
- d2
- N(d1)
- N(d2)

Using the formulas above, we can calculate the values of the call option and put option.

Calculating the Intermediate Variables

The intermediate variables d1 and d2 are calculated using the following formulas:

d1 = (ln(S/X) + (r + σ^2/2)T) / (σ * sqrt(T))

d2 = d1 - σ * sqrt(T)

Where:

ln is the natural logarithm
σ is the volatility

We can calculate the values of d1 and d2 using the following Excel formulas:

d1 = (LN(S/X) + (r + σ^2/2)*T) / (σ * SQRT(T))

d2 = d1 - σ * SQRT(T)

Calculating the Cumulative Distribution Functions

The cumulative distribution functions N(d1) and N(d2) can be calculated using the following Excel formulas:

N(d1) = NORM.S.DIST(d1, TRUE)

N(d2) = NORM.S.DIST(d2, TRUE)

Where:

NORM.S.DIST is the cumulative distribution function of the standard normal distribution

Calculating the Call Option and Put Option Values

Using the intermediate variables and cumulative distribution functions, we can calculate the values of the call option and put option using the following Excel formulas:

Call Option: C = S * N(d1) - X * EXP(-rT) * N(d2)

Put Option: P = X * EXP(-rT) * N(-d2) - S * N(-d1)

Where:

EXP is the exponential function

By following these steps, we can implement the Black-Scholes model in Excel and estimate the values of call options and put options.

Conclusion and Next Steps

In this article, we have explored how to implement the Black-Scholes model in Excel. By following the step-by-step guide, we can estimate the values of call options and put options using the formulas and intermediate variables.

However, the Black-Scholes model has its limitations, and it is essential to understand the assumptions and limitations of the model. In future articles, we will explore more advanced topics, such as the binomial model and the Monte Carlo simulation.

We hope this article has been helpful in understanding the Black-Scholes model and its implementation in Excel. If you have any questions or comments, please feel free to share them below.