Intro
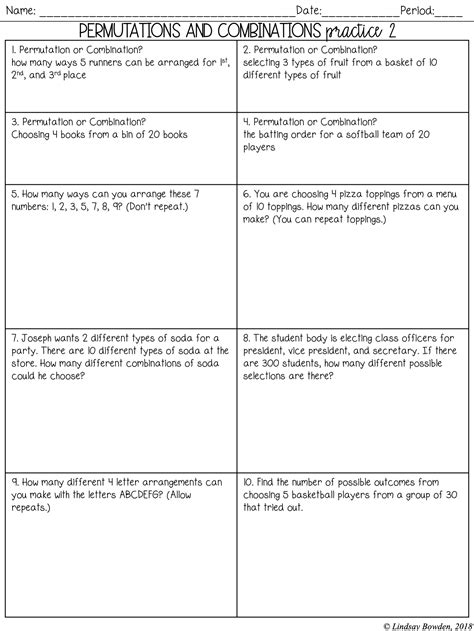
Master combinations and permutations with our in-depth worksheet answers guide. Learn the formulas and calculations behind 7 essential problems, covering topics like factorial notation, combination formulas, and permutation calculations. Enhance your math skills and understand the difference between combinations and permutations with our step-by-step explanations.
Combinations and permutations are fundamental concepts in mathematics, particularly in probability and statistics. These concepts help us calculate the number of ways to choose or arrange objects from a larger set. While often confused with each other, combinations and permutations have distinct differences, especially in their applications and calculations. In this article, we'll delve into the world of combinations and permutations, providing a comprehensive guide that includes explanations, examples, and detailed answers to commonly encountered problems.
Understanding Combinations
Combinations refer to the selection of items from a larger set, without regard to the order in which they are chosen. The formula to calculate combinations is given by C(n, r) = n! / [r!(n - r)!], where n is the total number of items, r is the number of items to choose, and "!" denotes factorial, which is the product of all positive integers up to that number.
Example 1: Combination Problem
Problem: In a class of 20 students, how many ways can a teacher select 5 students for a group project? Solution: Using the combination formula, C(20, 5) = 20! / [5!(20 - 5)!] = 15,504.

Understanding Permutations
Permutations involve the arrangement of objects in a specific order. The formula for permutations is P(n, r) = n! / (n - r)!, where n is the total number of objects, and r is the number of objects being chosen.
Example 2: Permutation Problem
Problem: How many ways can the letters in the word " пальто" be arranged? Solution: Since the word "пальто" has 6 letters, all distinct, the number of permutations is P(6, 6) = 6! = 720.
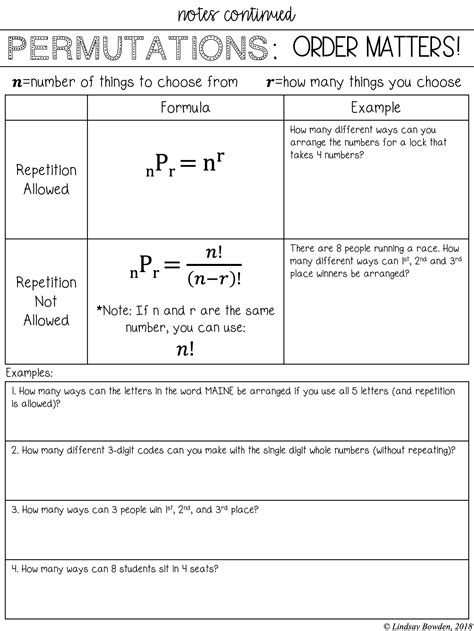
7 Combinations and Permutations Worksheet Answers Explained
-
Question: In a deck of 52 cards, how many ways can 5 cards be chosen for a hand?
- Answer: C(52, 5) = 52! / [5!(52 - 5)!] = 2,598,960.
-
Question: How many ways can the letters in the word "listen" be arranged?
- Answer: Since there are 6 letters and all are distinct, P(6, 6) = 6! = 720.
-
Question: From a group of 15 friends, how many ways can 3 be selected to attend a concert?
- Answer: C(15, 3) = 15! / [3!(15 - 3)!] = 455.
-
Question: A bookshelf has 8 books. How many ways can 4 books be arranged on it?
- Answer: P(8, 4) = 8! / (8 - 4)! = 8! / 4! = 1,680.
-
Question: In a class of 12 students, how many ways can a teacher choose 2 students for a presentation?
- Answer: C(12, 2) = 12! / [2!(12 - 2)!] = 66.
-
Question: How many ways can 6 people be seated around a circular table?
- Answer: Since it's a circular arrangement, (n-1)!, so for 6 people, it's (6-1)! = 5! = 120.
-
Question: From a bag of 10 different colored balls, how many ways can 3 balls be drawn without replacement?
- Answer: Since the order matters and there is no replacement, P(10, 3) = 10! / (10 - 3)! = 10! / 7! = 720.

Gallery of Combinations and Permutations Worksheet Answers Explained
Combinations and Permutations Worksheet Answers Explained Image Gallery



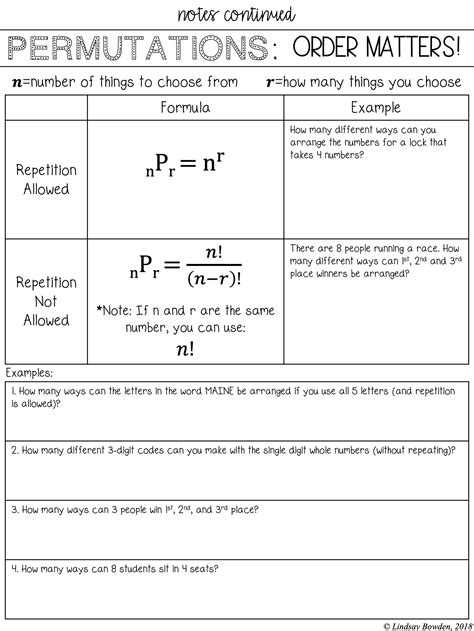





In conclusion, mastering combinations and permutations not only enhances your mathematical understanding but also equips you with critical thinking skills for problem-solving. Whether it's calculating the number of ways to select items from a set or arranging objects in a specific order, these concepts are fundamental in various fields, including statistics, computer science, and engineering. By practicing with the provided examples and understanding the formulas and explanations, you'll be well on your way to solving combinations and permutations problems with ease.
Feel free to share your thoughts or questions about combinations and permutations in the comments below. If you found this guide helpful, consider sharing it with others who might benefit from a comprehensive explanation of these mathematical concepts.
