Find Z-Score In Excel: Calculate Z/2 With Ease

Understanding the concept of Z-score is essential in statistics and data analysis. It measures the number of standard deviations a data point is away from the mean value of a dataset. Calculating Z-score in Excel is a straightforward process, and in this article, we will explore the steps to calculate Z-score and Z/2 in Excel with ease.

The Z-score is a dimensionless quantity that describes the distance between a value and the mean of a dataset, measured in terms of standard deviations. It is widely used in various fields such as finance, engineering, and quality control to identify outliers, detect anomalies, and make informed decisions.

Calculating Z-Score in Excel

To calculate the Z-score in Excel, you can use the following formula:

Z = (X - μ) / σ

Where:

• Z is the Z-score
• X is the value for which you want to calculate the Z-score
• μ is the mean of the dataset
• σ is the standard deviation of the dataset

Here's an example of how to calculate the Z-score in Excel:

Suppose we have a dataset of exam scores, and we want to calculate the Z-score for a specific score.

Score
80
75
90
85
70

To calculate the mean and standard deviation of the dataset, use the following formulas:

Mean: =AVERAGE(A1:A5) Standard Deviation: =STDEV(A1:A5)

Assuming the mean is 80 and the standard deviation is 7.07, we can calculate the Z-score for a score of 90 using the formula:

Z = (90 - 80) / 7.07 Z = 1.41

Using Excel Formulas to Calculate Z-Score

Excel provides several formulas to calculate the Z-score, including:

• STANDARDIZE function: This function calculates the Z-score for a given value, mean, and standard deviation.
• Z.TEST function: This function calculates the Z-score and the corresponding probability (p-value) for a given value, mean, and standard deviation.

The STANDARDIZE function has the following syntax:

STANDARDIZE(X, μ, σ)

Where:

• X is the value for which you want to calculate the Z-score
• μ is the mean of the dataset
• σ is the standard deviation of the dataset

The Z.TEST function has the following syntax:

Z.TEST(X, μ, σ)

Where:

• X is the value for which you want to calculate the Z-score
• μ is the mean of the dataset
• σ is the standard deviation of the dataset

Using these formulas, you can easily calculate the Z-score in Excel without having to use the manual formula.

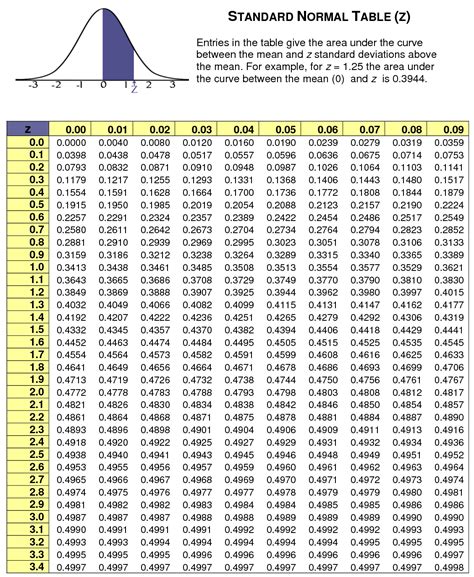
Calculating Z/2 in Excel

Z/2, also known as the two-tailed Z-score, is used to calculate the probability of observing a value at least as extreme as the given value, in either direction (i.e., above or below the mean).

To calculate Z/2 in Excel, you can use the following formula:

Z/2 = (X - μ) / (2 * σ)

Where:

• Z/2 is the two-tailed Z-score
• X is the value for which you want to calculate the Z/2 score
• μ is the mean of the dataset
• σ is the standard deviation of the dataset

Alternatively, you can use the Z.TEST function with the tails argument set to 2:

Z.TEST(X, μ, σ, 2)

This will return the two-tailed Z-score and the corresponding probability (p-value).

Example Use Cases

Z-scores have numerous applications in various fields. Here are a few examples:

• Quality Control: In manufacturing, Z-scores can be used to detect anomalies in product dimensions or quality. For instance, if the mean length of a product is 10 cm with a standard deviation of 0.5 cm, a Z-score of 2.5 would indicate that a product with a length of 12.5 cm is 2.5 standard deviations away from the mean.
• Finance: In finance, Z-scores can be used to evaluate the creditworthiness of borrowers. For example, a credit scoring model might use Z-scores to compare a borrower's credit score to the mean credit score of a population.
• Medical Research: In medical research, Z-scores can be used to compare the efficacy of different treatments. For instance, if the mean response to a treatment is 10 with a standard deviation of 2, a Z-score of 1.5 would indicate that a patient with a response of 12.5 is 1.5 standard deviations away from the mean.

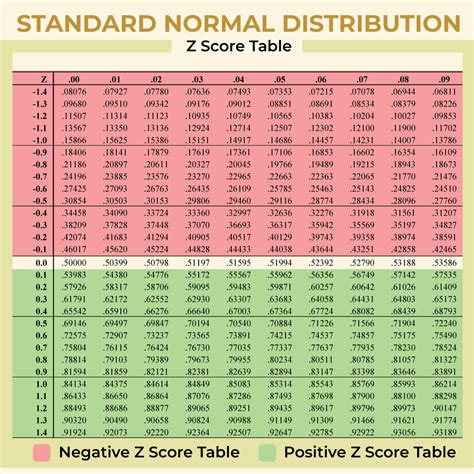
Frequently Asked Questions

Q: What is the difference between a Z-score and a standard deviation?

A: A Z-score measures the number of standard deviations a data point is away from the mean, while a standard deviation measures the amount of variation or dispersion in a dataset.

Q: How do I calculate the Z-score in Excel?

A: You can calculate the Z-score in Excel using the STANDARDIZE function or the Z.TEST function.

Q: What is the two-tailed Z-score (Z/2)?

A: The two-tailed Z-score (Z/2) is used to calculate the probability of observing a value at least as extreme as the given value, in either direction (i.e., above or below the mean).

Q: How do I calculate Z/2 in Excel?

A: You can calculate Z/2 in Excel using the Z.TEST function with the tails argument set to 2.

Gallery of Z-Score Related Topics

Z-Score Image Gallery

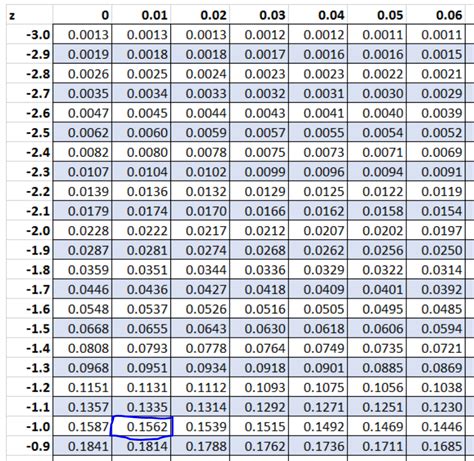
We hope this article has provided you with a comprehensive understanding of how to calculate Z-score in Excel. With these formulas and techniques, you can easily calculate Z-scores and Z/2 scores to analyze and interpret data in various fields.