Binary To Decimal Conversion Made Easy Worksheet

Converting binary to decimal is a fundamental concept in computer programming and mathematics. It's an essential skill for anyone working with computers, coding, or math. However, many people find it challenging to understand and apply this concept. In this article, we'll break down the process of binary to decimal conversion, making it easy and accessible for everyone.

Binary is a number system that uses only two digits: 0 and 1. It's the basis for all computer programming and is used to represent information, such as text, images, and instructions. Decimal, on the other hand, is the number system we use in our everyday lives, which includes the digits 0-9. Converting binary to decimal allows us to understand and work with binary code in a more familiar way.

Understanding Binary Numbers

Before we dive into the conversion process, let's quickly review how binary numbers work. Binary numbers are made up of bits, which can be either 0 or 1. Each bit has a place value, starting from the right. The place values are powers of 2, starting from 2^0, which is 1.

For example, the binary number 1010 can be broken down as follows:

• 1 (2^3) = 8
• 0 (2^2) = 0
• 1 (2^1) = 2
• 0 (2^0) = 0

Adding up the values, we get 8 + 2 = 10.

Converting Binary to Decimal

Now that we understand how binary numbers work, let's move on to the conversion process. There are several methods to convert binary to decimal, but we'll focus on the most common one.

Method 1: Using Place Values

This method involves multiplying each bit by its corresponding place value and adding up the results.

1. Write down the binary number.
2. Identify the place values for each bit, starting from the right.
3. Multiply each bit by its place value.
4. Add up the results.

For example, let's convert the binary number 1101 to decimal using this method:

• 1 (2^3) = 1 x 8 = 8
• 1 (2^2) = 1 x 4 = 4
• 0 (2^1) = 0 x 2 = 0
• 1 (2^0) = 1 x 1 = 1

Adding up the results, we get 8 + 4 + 1 = 13.

Method 2: Using a Calculator

If you have a calculator, you can use it to convert binary to decimal quickly and easily. Most calculators have a binary-to-decimal conversion function.

1. Enter the binary number into the calculator.
2. Press the binary-to-decimal conversion button.
3. Read the result.

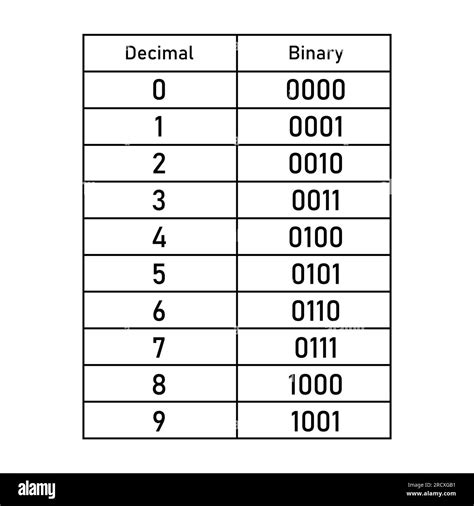
Binary to Decimal Conversion Table

If you don't have a calculator or prefer to use a table, you can use a binary-to-decimal conversion table. This table lists the binary numbers and their corresponding decimal values.

Binary	Decimal
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	10
...	...

Practice Exercises

Now that you've learned how to convert binary to decimal, it's time to practice! Here are some exercises to help you reinforce your understanding:

1. Convert the binary number 1011 to decimal.
2. Convert the binary number 1100 to decimal.
3. Convert the binary number 1001 to decimal.

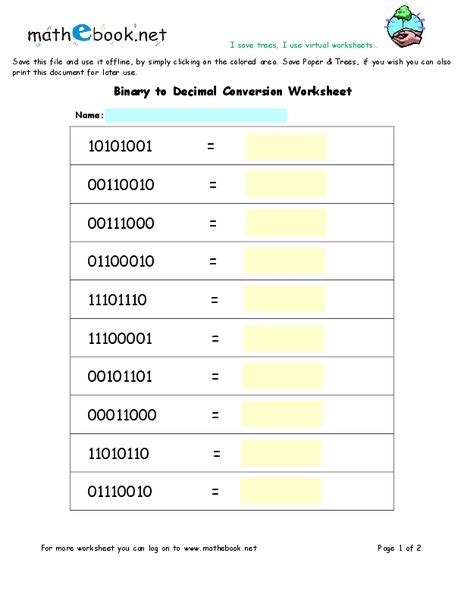
Binary to Decimal Conversion Worksheet

Here's a worksheet with 10 exercises to help you practice converting binary to decimal:

Binary	Decimal
1010	?
1101	?
1000	?
0111	?
1110	?
1011	?
1100	?
1001	?
0110	?
1111	?

Answer Key:

1. 10
2. 13
3. 8
4. 7
5. 14
6. 11
7. 12
8. 9
9. 6
10. 15

Gallery of Binary to Decimal Conversion

Binary to Decimal Conversion Gallery

Conclusion

Converting binary to decimal is a crucial skill in computer programming and mathematics. With practice and patience, you can master this skill and improve your understanding of binary numbers. Remember to use the place value method, calculator, or conversion table to make the process easier. Don't forget to practice with exercises and worksheets to reinforce your understanding.