Intro
Discover how to calculate sample size in Excel with ease. Learn 5 simple methods to determine sample size, including formulas and functions. Improve your statistical analysis skills and make informed decisions with accurate results. Master sample size calculation using Excels built-in tools and functions, including standard deviation, confidence intervals, and margin of error.
When conducting statistical analysis, determining the appropriate sample size is crucial to ensure that your results are reliable and representative of the population. In this article, we will explore five ways to calculate sample size in Excel.
In statistical analysis, sample size refers to the number of observations or data points used to represent a larger population. A larger sample size can provide more accurate results, but it also increases the time, cost, and complexity of the study. On the other hand, a small sample size may not accurately represent the population, leading to biased results.
Calculating the right sample size is essential to balance between accuracy and feasibility. In this article, we will discuss five methods to calculate sample size in Excel, along with their formulas and examples.
Method 1: Using the Sample Size Formula
One of the simplest ways to calculate sample size in Excel is to use the sample size formula. This formula is based on the margin of error, confidence level, and population standard deviation.
Formula: n = (Z^2 * σ^2) / E^2
Where: n = sample size Z = Z-score corresponding to the desired confidence level σ = population standard deviation E = margin of error
For example, let's say we want to calculate the sample size for a survey with a margin of error of 5%, a confidence level of 95%, and a population standard deviation of 10.
Image:

To calculate the sample size, we can use the following steps:
- Enter the Z-score corresponding to the desired confidence level (95% in this case).
- Enter the population standard deviation (10 in this case).
- Enter the margin of error (5% in this case).
- Use the formula = (Z^2 * σ^2) / E^2 to calculate the sample size.
Using this formula, we can calculate the sample size as follows:
= (1.96^2 * 10^2) / 0.05^2 = 384.16
Therefore, the required sample size is approximately 385.
Method 2: Using the Sample Size Calculator
Another way to calculate sample size in Excel is to use the built-in sample size calculator. This calculator is available in the "Data Analysis" toolbox.
Image:

To use the sample size calculator, follow these steps:
- Select the "Data Analysis" toolbox.
- Click on "Sample Size" under the "Statistical Analysis" section.
- Enter the desired confidence level, margin of error, and population standard deviation.
- Click "OK" to calculate the sample size.
Using this calculator, we can calculate the sample size as follows:
Confidence Level: 95% Margin of Error: 5% Population Standard Deviation: 10
The sample size calculator returns a sample size of approximately 385, which is consistent with the result obtained using the formula.
Method 3: Using the Power Analysis
Power analysis is another method to calculate sample size in Excel. This method involves calculating the power of the test, which is the probability of detecting a statistically significant effect.
Formula: n = (Z^2 * σ^2) / ( Effect Size^2 * (1 - Power))
Where: n = sample size Z = Z-score corresponding to the desired confidence level σ = population standard deviation Effect Size = effect size of the study Power = desired power of the test
For example, let's say we want to calculate the sample size for a study with a desired power of 80%, a confidence level of 95%, a population standard deviation of 10, and an effect size of 0.5.
Image:
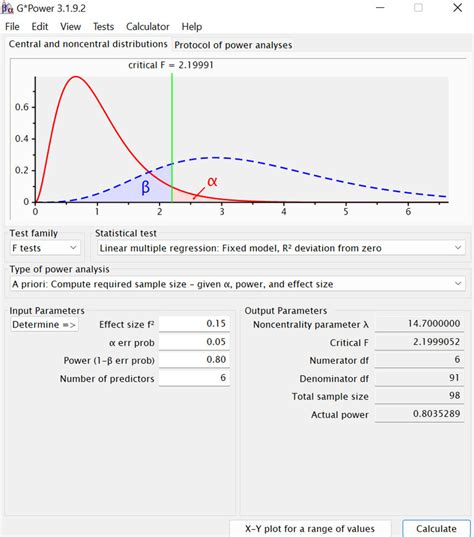
To calculate the sample size, we can use the following steps:
- Enter the Z-score corresponding to the desired confidence level (95% in this case).
- Enter the population standard deviation (10 in this case).
- Enter the effect size (0.5 in this case).
- Enter the desired power of the test (80% in this case).
- Use the formula = (Z^2 * σ^2) / ( Effect Size^2 * (1 - Power)) to calculate the sample size.
Using this formula, we can calculate the sample size as follows:
= (1.96^2 * 10^2) / ( 0.5^2 * (1 - 0.8)) = 246.92
Therefore, the required sample size is approximately 247.
Method 4: Using the Sample Size Formula for Proportions
When dealing with proportions, we can use a modified sample size formula to calculate the sample size.
Formula: n = (Z^2 * p * (1-p)) / E^2
Where: n = sample size Z = Z-score corresponding to the desired confidence level p = population proportion E = margin of error
For example, let's say we want to calculate the sample size for a survey with a margin of error of 5%, a confidence level of 95%, and a population proportion of 0.5.
Image:

To calculate the sample size, we can use the following steps:
- Enter the Z-score corresponding to the desired confidence level (95% in this case).
- Enter the population proportion (0.5 in this case).
- Enter the margin of error (5% in this case).
- Use the formula = (Z^2 * p * (1-p)) / E^2 to calculate the sample size.
Using this formula, we can calculate the sample size as follows:
= (1.96^2 * 0.5 * (1-0.5)) / 0.05^2 = 384.16
Therefore, the required sample size is approximately 385.
Method 5: Using the Sample Size Calculator for Proportions
Finally, we can use the built-in sample size calculator for proportions to calculate the sample size.
Image:

To use the sample size calculator for proportions, follow these steps:
- Select the "Data Analysis" toolbox.
- Click on "Sample Size for Proportions" under the "Statistical Analysis" section.
- Enter the desired confidence level, margin of error, and population proportion.
- Click "OK" to calculate the sample size.
Using this calculator, we can calculate the sample size as follows:
Confidence Level: 95% Margin of Error: 5% Population Proportion: 0.5
The sample size calculator returns a sample size of approximately 385, which is consistent with the result obtained using the formula.
Gallery of Sample Size Images:
Sample Size Image Gallery

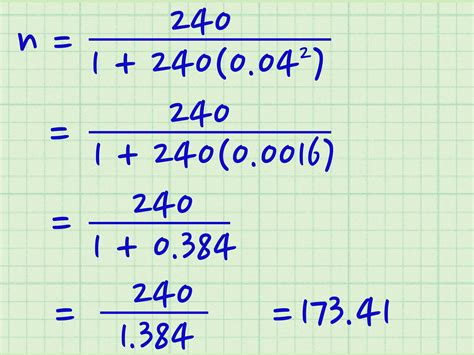



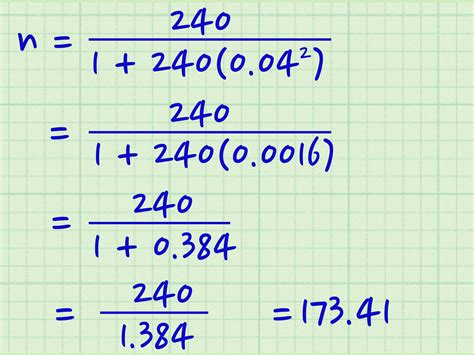

Conclusion:
Calculating the right sample size is crucial in statistical analysis to ensure that the results are reliable and representative of the population. In this article, we explored five methods to calculate sample size in Excel, including the sample size formula, sample size calculator, power analysis, sample size formula for proportions, and sample size calculator for proportions. By using these methods, researchers and analysts can determine the appropriate sample size for their studies and ensure that their results are accurate and reliable.
