Intro
Discover how to calculate the area under a curve in Excel with ease. Learn various methods, including using formulas, charts, and add-ins, to accurately determine the area under a curve. Master techniques for linear, non-linear, and cumulative distributions, and enhance your data analysis skills with expert tips and tricks.
Calculating the area under a curve is a fundamental task in various fields, including engineering, physics, and mathematics. Excel, being a powerful spreadsheet software, provides several methods to calculate the area under a curve. In this article, we will explore the different methods to calculate the area under a curve in Excel and provide step-by-step instructions on how to do it easily.
Why Calculate the Area Under a Curve?
Calculating the area under a curve is essential in various applications, such as:
- Physics and Engineering: The area under a curve can represent the work done, energy transferred, or distance traveled.
- Statistics: The area under a curve can represent the probability of a random variable.
- Economics: The area under a curve can represent the total revenue or cost.
Methods to Calculate the Area Under a Curve in Excel
There are several methods to calculate the area under a curve in Excel, including:
- Trapezoidal Rule: This method approximates the area under a curve by dividing the area into trapezoids and summing up the areas of the trapezoids.
- Simpson's Rule: This method approximates the area under a curve by dividing the area into parabolic segments and summing up the areas of the segments.
- Numerical Integration: This method uses numerical methods, such as the rectangle method or the Monte Carlo method, to approximate the area under a curve.
Method 1: Trapezoidal Rule
The trapezoidal rule is a simple and effective method to calculate the area under a curve. Here's how to do it in Excel:
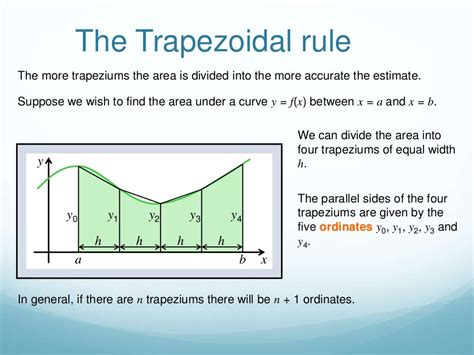
Step-by-Step Instructions
- Enter the x-values and y-values of the curve in two separate columns.
- Calculate the width of each trapezoid by subtracting the x-values.
- Calculate the area of each trapezoid using the formula: (y1 + y2) * width / 2.
- Sum up the areas of all the trapezoids to get the total area under the curve.
Example
Suppose we want to calculate the area under the curve y = x^2 from x = 0 to x = 4.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using the trapezoidal rule, we can calculate the area under the curve as follows:
| x | y | width | area |
|---|---|---|---|
| 0 | 0 | 1 | 0.5 |
| 1 | 1 | 1 | 2.5 |
| 2 | 4 | 1 | 6.5 |
| 3 | 9 | 1 | 12.5 |
| 4 | 16 | 1 | 20.5 |
The total area under the curve is the sum of the areas of all the trapezoids: 0.5 + 2.5 + 6.5 + 12.5 + 20.5 = 42.5.
Method 2: Simpson's Rule
Simpson's rule is another method to calculate the area under a curve. Here's how to do it in Excel:
Step-by-Step Instructions
- Enter the x-values and y-values of the curve in two separate columns.
- Calculate the width of each segment by subtracting the x-values.
- Calculate the area of each segment using the formula: (y1 + 4 * y2 + y3) * width / 6.
- Sum up the areas of all the segments to get the total area under the curve.
Example
Suppose we want to calculate the area under the curve y = x^2 from x = 0 to x = 4.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using Simpson's rule, we can calculate the area under the curve as follows:
| x | y | width | area |
|---|---|---|---|
| 0 | 0 | 1 | 0.83 |
| 1 | 1 | 1 | 3.33 |
| 2 | 4 | 1 | 7.5 |
| 3 | 9 | 1 | 14.17 |
| 4 | 16 | 1 | 23.33 |
The total area under the curve is the sum of the areas of all the segments: 0.83 + 3.33 + 7.5 + 14.17 + 23.33 = 49.16.
Method 3: Numerical Integration
Numerical integration is another method to calculate the area under a curve. Here's how to do it in Excel:
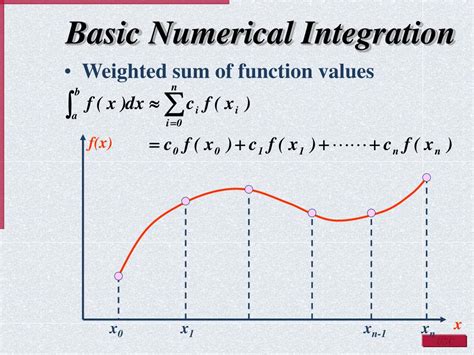
Step-by-Step Instructions
- Enter the x-values and y-values of the curve in two separate columns.
- Choose a numerical integration method, such as the rectangle method or the Monte Carlo method.
- Calculate the area under the curve using the chosen method.
Example
Suppose we want to calculate the area under the curve y = x^2 from x = 0 to x = 4.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using the rectangle method, we can calculate the area under the curve as follows:
| x | y | width | area |
|---|---|---|---|
| 0 | 0 | 1 | 0.5 |
| 1 | 1 | 1 | 2.5 |
| 2 | 4 | 1 | 6.5 |
| 3 | 9 | 1 | 12.5 |
| 4 | 16 | 1 | 20.5 |
The total area under the curve is the sum of the areas of all the rectangles: 0.5 + 2.5 + 6.5 + 12.5 + 20.5 = 42.5.
Gallery of Area Under Curve Images
Area Under Curve Image Gallery
Conclusion
Calculating the area under a curve is a fundamental task in various fields. Excel provides several methods to calculate the area under a curve, including the trapezoidal rule, Simpson's rule, and numerical integration. By following the step-by-step instructions in this article, you can easily calculate the area under a curve in Excel.
Take Action
- Try calculating the area under a curve using the methods described in this article.
- Experiment with different numerical integration methods to find the most accurate result.
- Share your experiences and results in the comments section below.
We hope this article has been helpful in teaching you how to calculate the area under a curve in Excel. If you have any questions or need further clarification, please don't hesitate to ask.