Antiderivative Of Trig Functions

The antiderivative of trig functions is a fundamental concept in calculus, playing a crucial role in understanding the behavior of trigonometric functions. Trigonometry, the study of triangles, has numerous applications in physics, engineering, and other fields. Calculus, which deals with the study of continuous change, is essential for modeling real-world phenomena. When we combine these two branches of mathematics, we enter the realm of trigonometric calculus, where finding antiderivatives of trig functions becomes essential. In this article, we will delve into the world of antiderivatives of trig functions, exploring their importance, methods of finding them, and practical applications.

The importance of antiderivatives cannot be overstated. An antiderivative, also known as an indefinite integral, represents a function whose derivative is the original function. For trigonometric functions, which describe the relationships between the sides and angles of triangles, finding antiderivatives is crucial for solving problems in physics, engineering, and other disciplines. These functions, such as sine, cosine, and tangent, are used to model periodic phenomena, like sound waves, light waves, and orbital motions. The antiderivative of these functions allows us to calculate areas under curves, volumes of solids, and other quantities that are essential in scientific and engineering applications.

Understanding the antiderivatives of trig functions requires a solid grasp of basic calculus concepts, including limits, derivatives, and integration rules. The derivative of a function represents the rate of change of the function with respect to its variable. Conversely, the antiderivative represents the accumulation of the function over a given interval. For trigonometric functions, we use specific integration rules, such as substitution, integration by parts, and trigonometric identities, to find their antiderivatives. These rules enable us to simplify complex trigonometric expressions and evaluate definite integrals, which are essential in solving problems in physics, engineering, and other fields.

Introduction to Antiderivatives of Trig Functions

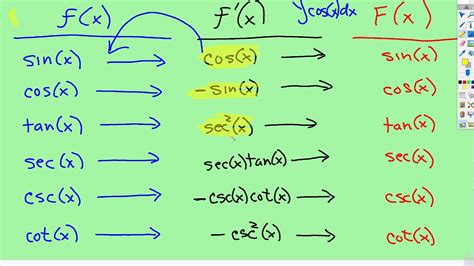
To find the antiderivative of a trig function, we need to understand the basic trigonometric functions and their derivatives. The most common trigonometric functions are sine (sin), cosine (cos), and tangent (tan). Their derivatives are:

The derivative of sin(x) is cos(x)
The derivative of cos(x) is -sin(x)
The derivative of tan(x) is sec^2(x)

Using these derivatives, we can find the antiderivatives of trig functions by applying integration rules. For example, to find the antiderivative of sin(x), we know that the derivative of -cos(x) is sin(x). Therefore, the antiderivative of sin(x) is -cos(x) + C, where C is the constant of integration.

Methods of Finding Antiderivatives of Trig Functions

There are several methods for finding antiderivatives of trig functions, including:

Substitution method: This method involves substituting a new variable or expression into the original function to simplify it.
Integration by parts: This method is used to integrate products of functions and is based on the product rule of differentiation.
Trigonometric identities: These identities, such as sin^2(x) + cos^2(x) = 1, can be used to simplify trigonometric expressions and find their antiderivatives.

By applying these methods, we can find the antiderivatives of various trig functions, including:

The antiderivative of cos(x) is sin(x) + C
The antiderivative of tan(x) is -ln|cos(x)| + C
The antiderivative of sec(x) is ln|sec(x) + tan(x)| + C

Practical Applications of Antiderivatives of Trig Functions

The antiderivatives of trig functions have numerous practical applications in physics, engineering, and other fields. Some examples include:

Simple harmonic motion: The antiderivative of sin(x) is used to model simple harmonic motion, such as the motion of a pendulum or a spring-mass system.
Electrical engineering: Trigonometric functions are used to model alternating current (AC) circuits, and their antiderivatives are essential for calculating quantities such as voltage, current, and power.
Signal processing: The antiderivatives of trig functions are used in signal processing techniques, such as filtering and modulation, to analyze and manipulate signals.

Benefits of Understanding Antiderivatives of Trig Functions

Understanding the antiderivatives of trig functions provides several benefits, including:

Improved problem-solving skills: By mastering the antiderivatives of trig functions, students can develop their problem-solving skills and become more proficient in solving complex calculus problems.
Enhanced understanding of physics and engineering concepts: The antiderivatives of trig functions are essential for understanding many physics and engineering concepts, such as simple harmonic motion, electrical circuits, and signal processing.
Better preparation for advanced math and science courses: A solid understanding of antiderivatives of trig functions prepares students for more advanced math and science courses, such as differential equations, linear algebra, and quantum mechanics.

Common Challenges and Misconceptions

When working with antiderivatives of trig functions, students often encounter common challenges and misconceptions, such as:

Difficulty with trigonometric identities: Students may struggle with applying trigonometric identities to simplify expressions and find antiderivatives.
Confusion with integration rules: The various integration rules, such as substitution and integration by parts, can be confusing, and students may struggle to apply them correctly.
Failure to check the answer: Students may forget to check their answer by differentiating the antiderivative to ensure that it is correct.

Best Practices for Learning Antiderivatives of Trig Functions

To learn antiderivatives of trig functions effectively, students should follow best practices, such as:

Practice consistently: Regular practice helps to develop problem-solving skills and build confidence.
Watch video tutorials and online lectures: Visual aids, such as video tutorials and online lectures, can help to clarify complex concepts and provide additional support.
Join a study group or discussion forum: Collaborating with peers can help to identify common challenges and misconceptions and provide opportunities for feedback and support.

Gallery of Antiderivative of Trig Functions

Antiderivative of Trig Functions Image Gallery

In conclusion, the antiderivative of trig functions is a fundamental concept in calculus with numerous applications in physics, engineering, and other fields. By understanding the antiderivatives of trig functions, students can develop their problem-solving skills, enhance their understanding of physics and engineering concepts, and prepare themselves for more advanced math and science courses. We encourage readers to share their thoughts and experiences with antiderivatives of trig functions in the comments section below. Additionally, we invite readers to explore other articles and resources on our website to further develop their knowledge of calculus and its applications.