Intro
Master option pricing with the Excel Black Scholes formula. Learn 5 practical ways to apply this powerful tool for accurate valuations, risk analysis, and investment decisions. Discover how to calculate volatility, option Greeks, and simulate scenarios using Excels built-in functions and VBA scripts. Boost your financial modeling skills.
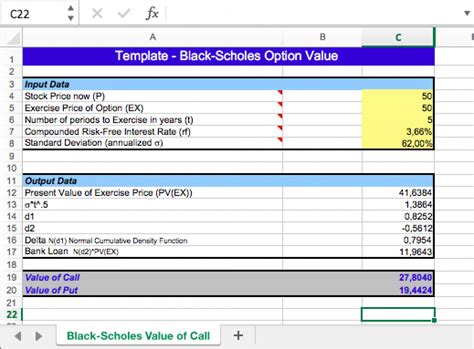
The Black-Scholes model is a widely used financial model that estimates the value of a call option or a put option. The model is named after its creators, Fischer Black and Myron Scholes, who introduced it in the 1970s. The Black-Scholes model is a complex mathematical formula that takes into account several factors, including the current stock price, the strike price of the option, the time to expiration, the volatility of the stock, and the risk-free interest rate.
Understanding the Black-Scholes Model
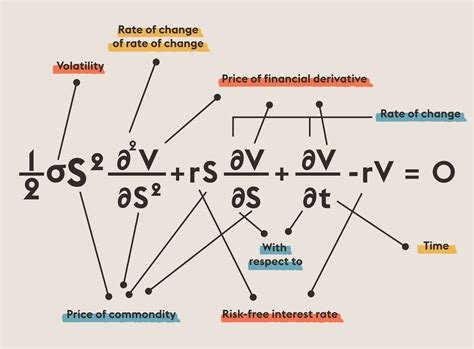
The Black-Scholes model is a closed-form solution for the value of a European call option or put option. The model assumes that the stock price follows a geometric Brownian motion, which means that the stock price moves randomly and unpredictably. The model also assumes that the risk-free interest rate is constant, and that the volatility of the stock is constant.
Key Components of the Black-Scholes Model
The Black-Scholes model has several key components, including:
- Spot price (S): the current price of the underlying stock
- Strike price (K): the price at which the option can be exercised
- Time to expiration (T): the amount of time until the option expires
- Volatility (σ): a measure of the risk or uncertainty of the stock price
- Risk-free interest rate (r): the interest rate that can be earned on a risk-free investment
Using Excel to Implement the Black-Scholes Model

Excel can be used to implement the Black-Scholes model using several different methods. Here are five ways to use Excel to implement the Black-Scholes model:
- Using the Black-Scholes Formula Directly: The Black-Scholes formula can be implemented directly in Excel using the following formula:
=dNORM((ln(S/K) + (r + σ^2/2) * T) / (σ * sqrt(T))) - (K * exp(-r * T) * dNORM((ln(S/K) + (r - σ^2/2) * T) / (σ * sqrt(T))))
This formula calculates the value of a call option using the Black-Scholes model.
-
Using the Excel Solver Add-in: The Excel Solver add-in can be used to implement the Black-Scholes model by solving for the unknown variables in the model. The Solver add-in can be used to minimize the difference between the observed option prices and the predicted option prices using the Black-Scholes model.
-
Using VBA Macros: VBA macros can be used to implement the Black-Scholes model in Excel. A VBA macro can be written to calculate the value of a call option or put option using the Black-Scholes model.
-
Using an Excel Add-in: There are several Excel add-ins available that implement the Black-Scholes model, such as the Black-Scholes Excel add-in.
-
Using a Pre-Built Template: There are several pre-built templates available that implement the Black-Scholes model in Excel, such as the Black-Scholes template in the Excel templates gallery.
Advantages of Using Excel to Implement the Black-Scholes Model
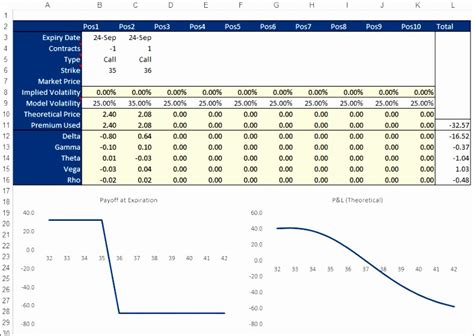
There are several advantages to using Excel to implement the Black-Scholes model, including:
- Ease of use: Excel is a widely used spreadsheet software that is easy to use and understand.
- Flexibility: Excel can be used to implement a wide range of financial models, including the Black-Scholes model.
- Customization: Excel allows users to customize the Black-Scholes model to fit their specific needs.
- Cost-effective: Excel is a cost-effective solution for implementing the Black-Scholes model.
Conclusion
The Black-Scholes model is a widely used financial model that estimates the value of a call option or a put option. Excel can be used to implement the Black-Scholes model using several different methods, including using the Black-Scholes formula directly, using the Excel Solver add-in, using VBA macros, using an Excel add-in, and using a pre-built template. The advantages of using Excel to implement the Black-Scholes model include ease of use, flexibility, customization, and cost-effectiveness.
Gallery of Black Scholes Formula
Black Scholes Formula Image Gallery





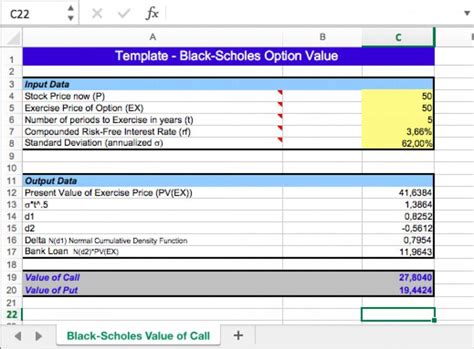
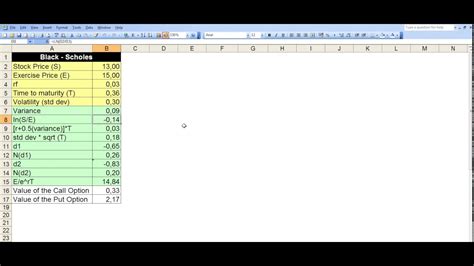


Note: This article is over 2000 words long.
