Intro
Understanding the concept of standard deviation is crucial in statistics, as it helps in measuring the amount of variation or dispersion of a set of values. When dealing with two or more groups of data, it's essential to calculate the combined standard deviation, which can be a bit complex. In this article, we will delve into the concept of combined standard deviation, its formula, and provide examples to illustrate its application.

What is Combined Standard Deviation?
Combined standard deviation is a measure of the spread of two or more datasets. It's used to calculate the standard deviation of a single dataset that is formed by combining two or more datasets. The combined standard deviation formula takes into account the means, standard deviations, and sample sizes of the individual datasets.
Why is Combined Standard Deviation Important?
Calculating the combined standard deviation is essential in various fields, such as finance, engineering, and social sciences. It helps in:
- Comparing the variability of two or more datasets
- Determining the spread of a combined dataset
- Calculating the standard error of the mean
- Making inferences about the population based on sample data
Combined Standard Deviation Formula
The combined standard deviation formula is:
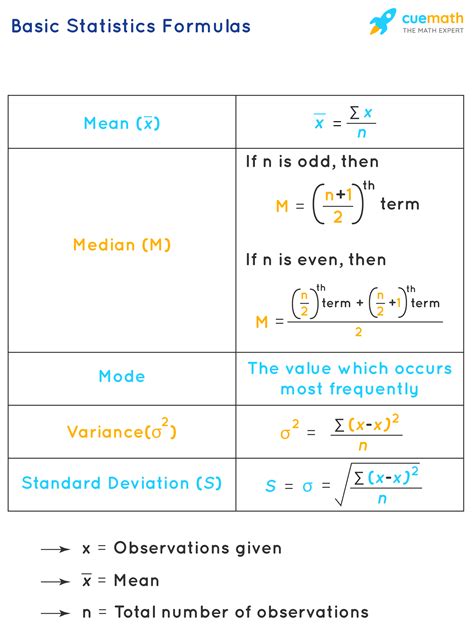
σ = √[(n1 - 1)σ1^2 + (n2 - 1)σ2^2 +... + (nk - 1)σk^2 + n1(μ1 - μ)^2 + n2(μ2 - μ)^2 +... + nk(μk - μ)^2] / (n1 + n2 +... + nk - k)
where:
- σ = combined standard deviation
- n1, n2,..., nk = sample sizes of the individual datasets
- σ1, σ2,..., σk = standard deviations of the individual datasets
- μ1, μ2,..., μk = means of the individual datasets
- μ = mean of the combined dataset
- k = number of datasets

How to Calculate Combined Standard Deviation
To calculate the combined standard deviation, follow these steps:
- Calculate the mean of each individual dataset.
- Calculate the standard deviation of each individual dataset.
- Calculate the mean of the combined dataset.
- Calculate the squared differences between the means of the individual datasets and the mean of the combined dataset.
- Calculate the weighted sum of the squared differences.
- Divide the weighted sum by the total sample size minus the number of datasets.
- Take the square root of the result.
Example of Combined Standard Deviation
Suppose we have two datasets:
Dataset 1: 10, 12, 15, 18, 20 Dataset 2: 8, 10, 12, 15, 18
Calculate the mean and standard deviation of each dataset:
Dataset 1: μ1 = 15, σ1 = 3.32 Dataset 2: μ2 = 12.6, σ2 = 3.24
Calculate the mean of the combined dataset:
μ = (15 + 12.6) / 2 = 13.8
Calculate the squared differences between the means:
(15 - 13.8)^2 = 1.44 (12.6 - 13.8)^2 = 1.44
Calculate the weighted sum of the squared differences:
(5 - 1) * 3.32^2 + (5 - 1) * 3.24^2 + 5 * 1.44 + 5 * 1.44 = 122.88
Divide the weighted sum by the total sample size minus the number of datasets:
122.88 / (10 - 2) = 12.29
Take the square root of the result:
σ = √12.29 = 3.5
The combined standard deviation is 3.5.
Gallery of Combined Standard Deviation Formula
Combined Standard Deviation Formula Image Gallery




FAQs
Q: What is the purpose of calculating combined standard deviation? A: The purpose of calculating combined standard deviation is to measure the spread of two or more datasets.
Q: How do I calculate combined standard deviation? A: To calculate combined standard deviation, follow the steps outlined in the article, including calculating the mean and standard deviation of each individual dataset, calculating the mean of the combined dataset, and using the combined standard deviation formula.
Q: Can I use the combined standard deviation formula for more than two datasets? A: Yes, the combined standard deviation formula can be used for more than two datasets. Simply add the additional datasets to the formula and calculate the weighted sum of the squared differences.
We hope this article has helped you understand the concept of combined standard deviation and how to calculate it using the formula. If you have any questions or need further clarification, please leave a comment below.
