Intro
Simplify fractions easily with 5 proven methods, mastering equivalent ratios, decimal conversions, and basic algebra to reduce complex math problems into manageable parts.
Simplifying fractions is an essential skill in mathematics, as it helps to reduce complex fractions to their most basic form, making them easier to work with. Fractions are used to represent parts of a whole, and simplifying them is crucial in various mathematical operations, such as addition, subtraction, multiplication, and division. In this article, we will explore the importance of simplifying fractions and provide 5 ways to simplify them.
Simplifying fractions is important because it helps to avoid confusion and errors in mathematical calculations. When fractions are not simplified, they can be difficult to compare and operate on, leading to incorrect results. For instance, if you have two fractions, 2/4 and 1/2, they may look different, but they actually represent the same value. By simplifying fractions, you can easily identify equivalent fractions and perform operations with accuracy.
Simplifying fractions also helps to reduce the complexity of mathematical expressions and equations. When fractions are simplified, they become easier to work with, and mathematical operations become more straightforward. For example, if you need to add two fractions, 3/6 and 2/4, simplifying them to 1/2 and 1/2, respectively, makes the addition process much simpler.
Introduction to Simplifying Fractions

Simplifying fractions involves reducing the numerator and denominator of a fraction to their smallest possible values while maintaining the same value. This process involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both numbers by the GCD. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
5 Ways to Simplify Fractions

Here are 5 ways to simplify fractions:
- Find the greatest common divisor (GCD) of the numerator and denominator and divide both numbers by the GCD.
- Use the prime factorization method to simplify fractions.
- Simplify fractions by canceling out common factors between the numerator and denominator.
- Use the division method to simplify fractions.
- Simplify fractions by using equivalent ratios.
Method 1: Finding the Greatest Common Divisor (GCD)
The first method involves finding the GCD of the numerator and denominator and dividing both numbers by the GCD. For example, if you have the fraction 6/8, you can find the GCD of 6 and 8, which is 2. Then, you divide both numbers by 2 to get the simplified fraction 3/4.
Method 2: Prime Factorization

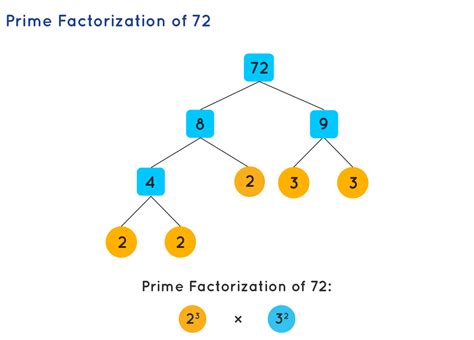
The second method involves using prime factorization to simplify fractions. Prime factorization involves breaking down numbers into their prime factors. For example, if you have the fraction 12/16, you can break down 12 into its prime factors, which are 2 x 2 x 3, and 16 into its prime factors, which are 2 x 2 x 2 x 2. Then, you can cancel out common prime factors between the numerator and denominator to get the simplified fraction 3/4.
Method 3: Canceling Out Common Factors

The third method involves canceling out common factors between the numerator and denominator. For example, if you have the fraction 9/12, you can cancel out the common factor 3 between the numerator and denominator to get the simplified fraction 3/4.
Method 4: Division Method

The fourth method involves using the division method to simplify fractions. This method involves dividing the numerator by the denominator and finding the remainder. For example, if you have the fraction 7/9, you can divide 7 by 9 to get a quotient of 0 and a remainder of 7. Then, you can write the fraction as 0 7/9, which is already in its simplest form.
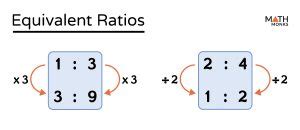
Method 5: Equivalent Ratios
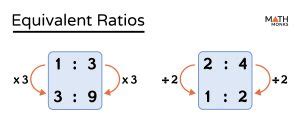
The fifth method involves using equivalent ratios to simplify fractions. Equivalent ratios are fractions that have the same value but different numerators and denominators. For example, if you have the fraction 2/3, you can multiply both the numerator and denominator by 2 to get the equivalent ratio 4/6. Then, you can simplify the fraction 4/6 by dividing both numbers by their GCD, which is 2, to get the simplified fraction 2/3.
Benefits of Simplifying Fractions
Simplifying fractions has several benefits, including:
- Easier comparison of fractions
- Simplified mathematical operations
- Reduced complexity of mathematical expressions and equations
- Improved accuracy in mathematical calculations
- Enhanced understanding of mathematical concepts
Common Challenges in Simplifying Fractions

Despite the importance of simplifying fractions, many students and individuals face challenges in this area. Some common challenges include:
- Difficulty in finding the GCD of the numerator and denominator
- Inability to cancel out common factors between the numerator and denominator
- Lack of understanding of equivalent ratios
- Difficulty in applying the division method
- Inability to simplify complex fractions
Gallery of Fraction Simplification
Fraction Simplification Image Gallery







Final Thoughts

In conclusion, simplifying fractions is an essential skill in mathematics that can help reduce complex fractions to their most basic form, making them easier to work with. By using the 5 methods outlined in this article, individuals can simplify fractions with ease and accuracy. Whether you are a student or an individual looking to improve your mathematical skills, simplifying fractions is a crucial concept to master. We encourage you to practice simplifying fractions using the methods outlined in this article and to share your thoughts and experiences with us.
