Intro
Discover 3 easy methods to calculate the area under a curve in Excel. Learn how to use numerical integration, graphing, and formula-based approaches to find the area under curves, including the normal distribution curve, in Excel. Master AUC calculations with our step-by-step guide and unlock data analysis insights.
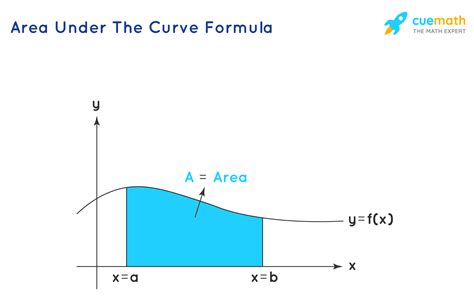
Calculating the area under a curve in Excel can be a valuable skill, especially for those in fields such as finance, engineering, and economics. The area under a curve can represent various quantities, such as the accumulation of a quantity over time or the probability of a certain event occurring. In this article, we will explore three methods to calculate the area under a curve in Excel.
Method 1: Using the Trapezoidal Rule
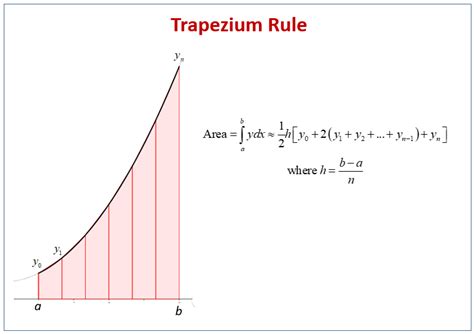
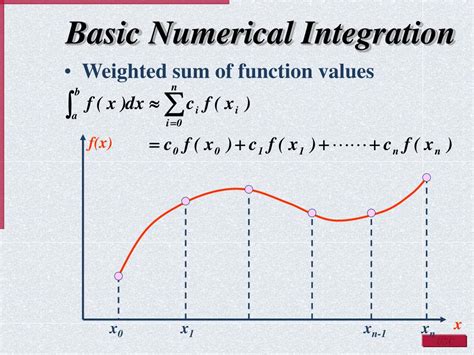
The trapezoidal rule is a numerical method for approximating the area under a curve. This method involves dividing the area into small trapezoids and summing the areas of the trapezoids. To apply the trapezoidal rule in Excel, follow these steps:
- Create a table with the x-values and corresponding y-values.
- Calculate the width of each trapezoid by subtracting the x-values.
- Calculate the area of each trapezoid using the formula: (y1 + y2) / 2 * width.
- Sum the areas of all trapezoids to get the total area under the curve.
You can use the following Excel formula to calculate the area under the curve using the trapezoidal rule:
=SUM((A2:A10+B2:B10)/2*(B2:B10-A2:A10))
where A2:A10 and B2:B10 are the ranges containing the x-values and y-values, respectively.
Advantages and Limitations of the Trapezoidal Rule
The trapezoidal rule is a simple and intuitive method for approximating the area under a curve. However, it can be less accurate than other methods, especially for curves with high curvature or rapidly changing slopes. Additionally, the trapezoidal rule requires a large number of trapezoids to achieve high accuracy, which can be computationally intensive.
Method 2: Using the Simpson's Rule
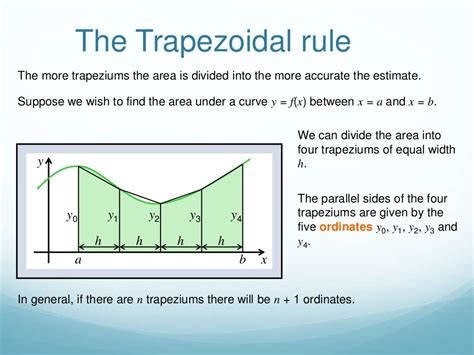
Simpson's rule is another numerical method for approximating the area under a curve. This method involves dividing the area into small parabolic segments and summing the areas of the segments. To apply Simpson's rule in Excel, follow these steps:
- Create a table with the x-values and corresponding y-values.
- Calculate the width of each segment by subtracting the x-values.
- Calculate the area of each segment using the formula: (y1 + 4*y2 + y3) / 6 * width.
- Sum the areas of all segments to get the total area under the curve.
You can use the following Excel formula to calculate the area under the curve using Simpson's rule:
=SUM((A2:A10+4*B2:B10+C2:C10)/6*(B2:B10-A2:A10))
where A2:A10, B2:B10, and C2:C10 are the ranges containing the x-values and y-values, respectively.
Advantages and Limitations of Simpson's Rule
Simpson's rule is generally more accurate than the trapezoidal rule, especially for curves with high curvature or rapidly changing slopes. However, Simpson's rule requires a larger number of segments to achieve high accuracy, which can be computationally intensive.
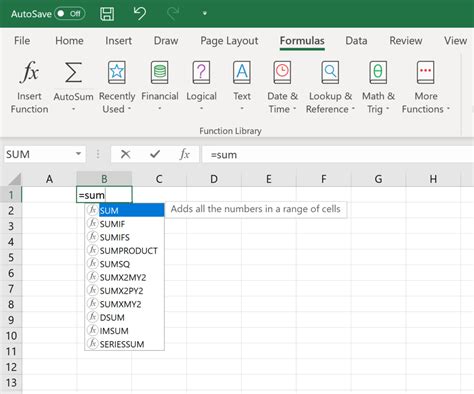
Method 3: Using the Built-in Excel Function
Excel provides a built-in function for calculating the area under a curve, called the intégrate function. This function uses a sophisticated algorithm to approximate the area under the curve. To use the intégrate function, follow these steps:
- Create a table with the x-values and corresponding y-values.
- Select the range containing the x-values and y-values.
- Go to the "Formulas" tab in the ribbon and click on the "Math & Trig" button.
- Select the " intégrate" function from the drop-down menu.
- Enter the range containing the x-values and y-values as the input.
- Click "OK" to calculate the area under the curve.
The intégrate function is generally more accurate and efficient than the trapezoidal rule and Simpson's rule. However, it may not be suitable for curves with high curvature or rapidly changing slopes.
Advantages and Limitations of the Built-in Excel Function
The built-in Excel function is a convenient and efficient way to calculate the area under a curve. However, it may not be suitable for curves with high curvature or rapidly changing slopes. Additionally, the function may not provide the same level of accuracy as other methods, such as Simpson's rule.
Area Under Curve Image Gallery
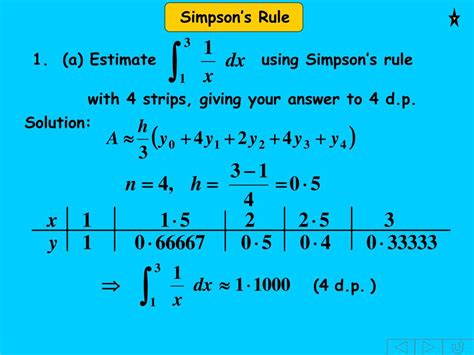
In conclusion, calculating the area under a curve in Excel can be achieved using various methods, including the trapezoidal rule, Simpson's rule, and the built-in Excel function. Each method has its advantages and limitations, and the choice of method depends on the specific requirements of the problem. We hope this article has provided you with a comprehensive understanding of the different methods for calculating the area under a curve in Excel. If you have any questions or need further clarification, please leave a comment below.