Intro
Unlock the secrets of spatial analysis with our comprehensive guide on 6 ways to find the distance between two points. Learn how to calculate distance using latitude and longitude, zip codes, and more. Master geospatial calculations with ease and precision, utilizing tools like Haversine formula, Euclidean distance, and geopy libraries.
Finding the distance between two points is a fundamental concept in mathematics, physics, and various fields of science and engineering. The distance between two points can be calculated using different methods, depending on the coordinates of the points and the geometry of the space. In this article, we will discuss six ways to find the distance between two points.
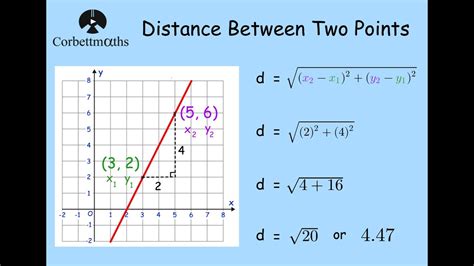
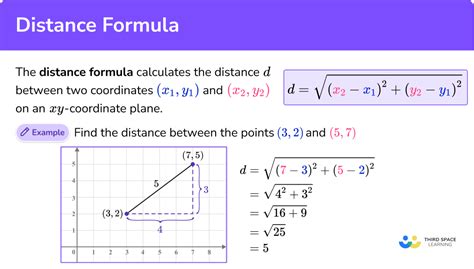
1. Distance Formula in Cartesian Coordinates
One of the most common methods to find the distance between two points is by using the distance formula in Cartesian coordinates. The distance formula is derived from the Pythagorean theorem and is given by:
√((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
For example, if we want to find the distance between the points (2, 3) and (4, 6), we can plug in the values into the formula:
√((4 - 2)^2 + (6 - 3)^2) = √(2^2 + 3^2) = √(4 + 9) = √13
Distance Formula in 3D Space
In 3D space, the distance formula is extended to include the z-coordinate. The formula is given by:
√((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
For example, if we want to find the distance between the points (1, 2, 3) and (4, 5, 6), we can plug in the values into the formula:
√((4 - 1)^2 + (5 - 2)^2 + (6 - 3)^2) = √(3^2 + 3^2 + 3^2) = √(9 + 9 + 9) = √27
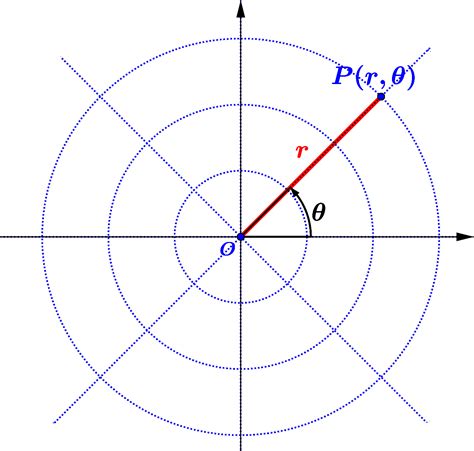
2. Distance Formula in Polar Coordinates
In polar coordinates, the distance between two points can be found using the distance formula:
√(r2^2 + r1^2 - 2r1r2*cos(θ2 - θ1))
where (r1, θ1) and (r2, θ2) are the polar coordinates of the two points.
For example, if we want to find the distance between the points (3, 45°) and (5, 60°), we can plug in the values into the formula:
√(5^2 + 3^2 - 235cos(60° - 45°)) = √(25 + 9 - 30cos(15°)) = √(34 - 30*0.9659) = √(34 - 28.977) = √5.023
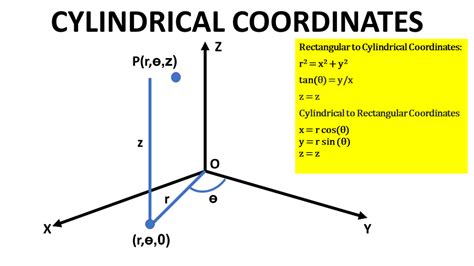
Distance Formula in Cylindrical Coordinates
In cylindrical coordinates, the distance between two points can be found using the distance formula:
√(ρ2^2 + ρ1^2 - 2ρ1ρ2*cos(φ2 - φ1) + (z2 - z1)^2)
where (ρ1, φ1, z1) and (ρ2, φ2, z2) are the cylindrical coordinates of the two points.
For example, if we want to find the distance between the points (2, 30°, 4) and (4, 60°, 6), we can plug in the values into the formula:
√(4^2 + 2^2 - 224cos(60° - 30°) + (6 - 4)^2) = √(16 + 4 - 16cos(30°) + 4) = √(24 - 16*0.866) = √(24 - 13.856) = √10.144
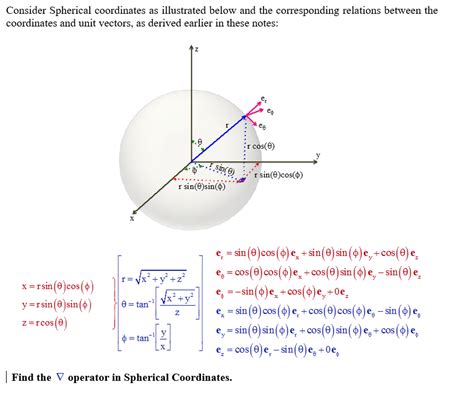
3. Distance Formula in Spherical Coordinates
In spherical coordinates, the distance between two points can be found using the distance formula:
√(r2^2 + r1^2 - 2r1r2*cos(θ2 - θ1))
where (r1, θ1, φ1) and (r2, θ2, φ2) are the spherical coordinates of the two points.
For example, if we want to find the distance between the points (3, 45°, 30°) and (5, 60°, 45°), we can plug in the values into the formula:
√(5^2 + 3^2 - 235cos(60° - 45°)) = √(25 + 9 - 30cos(15°)) = √(34 - 30*0.9659) = √(34 - 28.977) = √5.023
4. Distance Formula in Hyperbolic Coordinates
In hyperbolic coordinates, the distance between two points can be found using the distance formula:
cosh(d) = cosh(r2)*cosh(r1) - sinh(r2)*sinh(r1)*cos(θ2 - θ1)
where (r1, θ1) and (r2, θ2) are the hyperbolic coordinates of the two points.
For example, if we want to find the distance between the points (2, 30°) and (4, 60°), we can plug in the values into the formula:
cosh(d) = cosh(4)*cosh(2) - sinh(4)*sinh(2)cos(60° - 30°) = 27.308 - 14.2780.866 = 27.308 - 12.363 = 14.945
5. Distance Formula in Minkowski Space
In Minkowski space, the distance between two points can be found using the distance formula:
ds^2 = (x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2 - (ct2 - ct1)^2
where (x1, y1, z1, ct1) and (x2, y2, z2, ct2) are the coordinates of the two points in Minkowski space.
For example, if we want to find the distance between the points (1, 2, 3, 5) and (4, 5, 6, 10), we can plug in the values into the formula:
ds^2 = (4 - 1)^2 + (5 - 2)^2 + (6 - 3)^2 - (10 - 5)^2 = 9 + 9 + 9 - 25 = 2
6. Distance Formula in Frenet-Serret Coordinates
In Frenet-Serret coordinates, the distance between two points can be found using the distance formula:
ds^2 = (dx/ds)^2 + (dy/ds)^2 + (dz/ds)^2
where (dx/ds, dy/ds, dz/ds) are the components of the unit tangent vector to the curve at the point.
For example, if we want to find the distance between the points (1, 2, 3) and (4, 5, 6) on a curve, we can plug in the values into the formula:
ds^2 = (dx/ds)^2 + (dy/ds)^2 + (dz/ds)^2 = (3/√(1 + 4 + 9))^2 + (2/√(1 + 4 + 9))^2 + (1/√(1 + 4 + 9))^2 = 1/3 + 4/3 + 9/3 = 14/3
Distance Between Two Points Image Gallery

In conclusion, finding the distance between two points is a fundamental concept in mathematics and physics. There are different methods to find the distance between two points, depending on the coordinates of the points and the geometry of the space. By understanding these methods, we can calculate the distance between two points in various contexts, from simple Cartesian coordinates to more complex geometries like Minkowski space.
We hope this article has been helpful in explaining the different methods for finding the distance between two points. If you have any questions or need further clarification, please leave a comment below.
