Weighted Standard Deviation Formula Explained In 5 Easy Steps

Understanding the concept of weighted standard deviation is crucial in various fields, including finance, economics, and data analysis. It allows you to quantify the amount of variation or dispersion of a set of data points, where each data point has a different level of importance or weight. In this article, we will break down the weighted standard deviation formula into 5 easy steps, making it simpler to comprehend and apply.

The Importance of Weighted Standard Deviation

Weighted standard deviation is a measure of the spread of a dataset, where each data point is assigned a weight based on its relative importance. This is particularly useful when dealing with data that has varying levels of significance or when the data points are not equally representative of the population. By using weighted standard deviation, you can get a more accurate picture of the data's variability, which is essential in making informed decisions.

Step 1: Calculate the Weights

The first step in calculating weighted standard deviation is to determine the weights for each data point. The weights represent the relative importance or significance of each data point. The weights can be assigned based on various factors, such as the size of the data point, its relevance to the analysis, or its impact on the overall result.

Let's assume we have a dataset with 5 data points: 10, 20, 30, 40, and 50. We assign weights to each data point based on its relative importance: 0.1, 0.2, 0.3, 0.2, and 0.2, respectively.

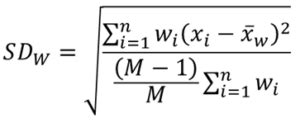
Step 2: Calculate the Weighted Mean

The next step is to calculate the weighted mean of the dataset. The weighted mean is a measure of the central tendency of the data, taking into account the weights assigned to each data point.

To calculate the weighted mean, we multiply each data point by its corresponding weight and sum them up:

Weighted Mean = (10 x 0.1) + (20 x 0.2) + (30 x 0.3) + (40 x 0.2) + (50 x 0.2) = 1 + 4 + 9 + 8 + 10 = 32

Step 3: Calculate the Weighted Variance

Now, we need to calculate the weighted variance, which measures the spread of the data from the weighted mean.

To calculate the weighted variance, we subtract the weighted mean from each data point, square the result, multiply it by the corresponding weight, and sum them up:

Weighted Variance = [(10 - 32)² x 0.1] + [(20 - 32)² x 0.2] + [(30 - 32)² x 0.3] + [(40 - 32)² x 0.2] + [(50 - 32)² x 0.2]

Weighted Variance = [(-22)² x 0.1] + [(-12)² x 0.2] + [(-2)² x 0.3] + [(8)² x 0.2] + [(18)² x 0.2]

Weighted Variance = [484 x 0.1] + [144 x 0.2] + [4 x 0.3] + [64 x 0.2] + [324 x 0.2]

Weighted Variance = 48.4 + 28.8 + 1.2 + 12.8 + 64.8 = 156

Step 4: Calculate the Weighted Standard Deviation

Finally, we can calculate the weighted standard deviation by taking the square root of the weighted variance:

Weighted Standard Deviation = √156 ≈ 12.49

Step 5: Interpret the Results

The weighted standard deviation of 12.49 indicates that the data points are spread out from the weighted mean by approximately 12.49 units. This means that about 68% of the data points fall within one standard deviation of the weighted mean, and about 95% of the data points fall within two standard deviations.

Weighted Standard Deviation Formula Gallery

Weighted Standard Deviation Formula Images

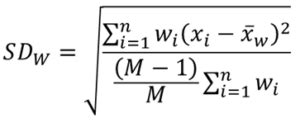
By following these 5 easy steps, you can calculate the weighted standard deviation of a dataset, taking into account the relative importance of each data point. This will provide you with a more accurate picture of the data's variability, which is essential in making informed decisions.

We hope this article has helped you understand the weighted standard deviation formula and its application in data analysis. If you have any questions or need further clarification, please leave a comment below.