5 Ways To Check For Normality In Excel

Normality is a fundamental assumption in many statistical tests, including regression analysis, t-tests, and ANOVA. It is essential to check for normality before conducting these tests to ensure the accuracy of the results. Excel provides several methods to check for normality, and in this article, we will discuss five ways to do so.

Understanding Normality

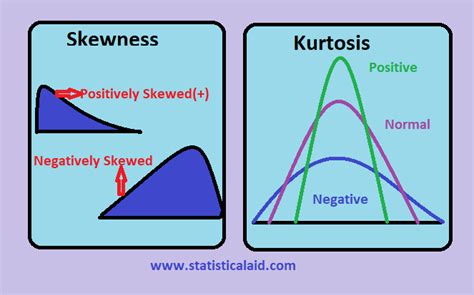
Normality refers to the distribution of data that follows a bell-shaped curve, also known as a Gaussian distribution. In a normal distribution, the majority of the data points cluster around the mean, and the farther away from the mean, the fewer data points there are. Normality is essential in statistics because many statistical tests assume that the data follows a normal distribution.

Why Check for Normality?

Checking for normality is crucial because many statistical tests are sensitive to non-normality. If the data is not normally distributed, the results of the statistical test may not be accurate. For example, if the data is skewed or has outliers, the mean and standard deviation may not accurately represent the data, leading to incorrect conclusions.

Method 1: Histograms

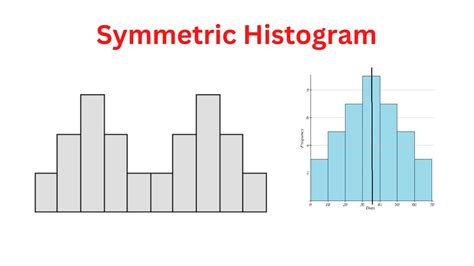
One of the simplest ways to check for normality is by creating a histogram. A histogram is a graphical representation of the distribution of data. To create a histogram in Excel, follow these steps:

• Select the data range
• Go to the "Insert" tab
• Click on "Chart"
• Select "Histogram"

A histogram will display the distribution of the data. If the data is normally distributed, the histogram should resemble a bell-shaped curve.

Interpreting Histograms

When interpreting histograms, look for the following characteristics of a normal distribution:

• The histogram should be symmetric around the mean
• The majority of the data points should cluster around the mean
• The farther away from the mean, the fewer data points there should be

Method 2: Q-Q Plots

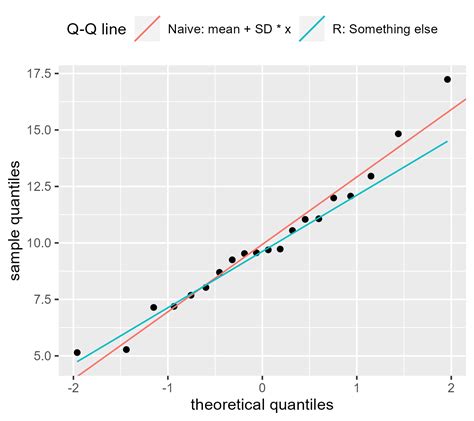
A Q-Q plot, also known as a quantile-quantile plot, is a graphical method for comparing the distribution of two datasets. In this case, we will compare the distribution of our data to a normal distribution. To create a Q-Q plot in Excel, follow these steps:

• Select the data range
• Go to the "Insert" tab
• Click on "Chart"
• Select "Scatter"

Plot the data against a normal distribution using the following formula:

=NORMSINV((ROW(A1)-0.5)/COUNT(A:A))

Where A1 is the first cell in the data range.

Interpreting Q-Q Plots

When interpreting Q-Q plots, look for the following characteristics of a normal distribution:

• The points should lie close to a straight line
• The line should be approximately 45 degrees
• There should be no systematic deviations from the line

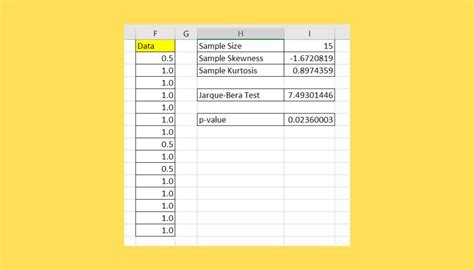
Method 3: Skewness and Kurtosis

Skewness and kurtosis are statistical measures that can help determine if the data is normally distributed. Skewness measures the asymmetry of the distribution, while kurtosis measures the "tailedness" of the distribution.

To calculate skewness and kurtosis in Excel, use the following formulas:

Skewness:

=SKEW(A1:A100)

Kurtosis:

=KURT(A1:A100)

Where A1:A100 is the data range.

Interpreting Skewness and Kurtosis

When interpreting skewness and kurtosis, look for the following values:

• Skewness: close to 0 (±1)
• Kurtosis: close to 3 (±1)

Values outside of these ranges may indicate non-normality.

Method 4: Shapiro-Wilk Test

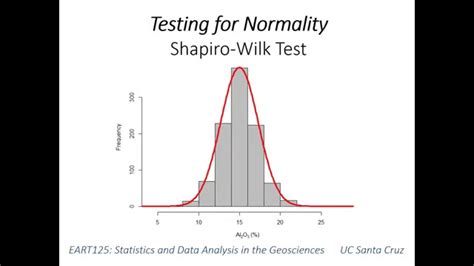
The Shapiro-Wilk test is a statistical test that can be used to determine if the data is normally distributed. To perform the Shapiro-Wilk test in Excel, use the following formula:

=IF(SIGMA.S.WILK(A1:A100)>0.05,"Normal","Non-Normal")

Where A1:A100 is the data range.

Interpreting Shapiro-Wilk Test

When interpreting the Shapiro-Wilk test, look for the following values:

• If the p-value is greater than 0.05, the data is likely normally distributed
• If the p-value is less than 0.05, the data is likely not normally distributed

Method 5: Anderson-Darling Test

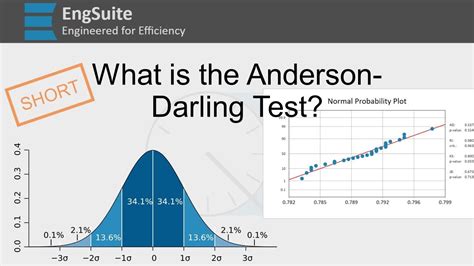
The Anderson-Darling test is another statistical test that can be used to determine if the data is normally distributed. To perform the Anderson-Darling test in Excel, use the following formula:

=IF(ANDERSON.DARLING(A1:A100)>0.05,"Normal","Non-Normal")

Where A1:A100 is the data range.

Interpreting Anderson-Darling Test

When interpreting the Anderson-Darling test, look for the following values:

• If the p-value is greater than 0.05, the data is likely normally distributed
• If the p-value is less than 0.05, the data is likely not normally distributed

Normality Tests Image Gallery

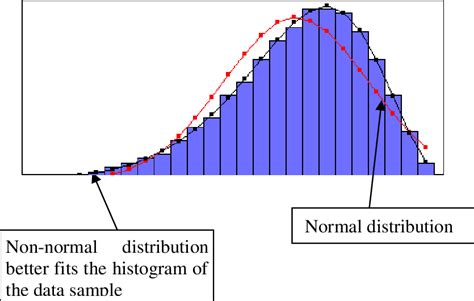
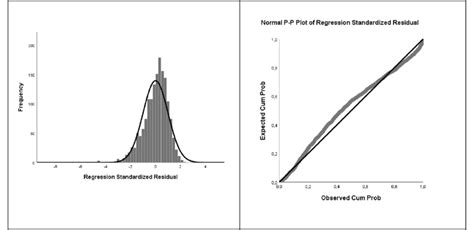
We hope this article has provided you with a comprehensive understanding of the five ways to check for normality in Excel. By using these methods, you can determine if your data is normally distributed and ensure the accuracy of your statistical tests. Remember to always check for normality before conducting statistical tests, and to use a combination of methods to confirm your results.

What's your experience with checking for normality in Excel? Share your thoughts and questions in the comments below!