Numerical Integration In Excel: A Step-By-Step Guide

Numerical integration is a fundamental concept in mathematics and engineering, and it's widely used in various fields, including physics, economics, and computer science. In simple terms, numerical integration is a method of approximating the value of a definite integral using numerical methods. While there are many software packages and programming languages that can be used for numerical integration, Microsoft Excel is a popular choice due to its widespread availability and user-friendly interface. In this article, we'll provide a step-by-step guide on how to perform numerical integration in Excel.

Why Use Numerical Integration in Excel?

There are several reasons why you might want to use numerical integration in Excel:

• Simplicity: Excel is a widely used software package that's easy to learn and use, even for those without extensive programming experience.
• Flexibility: Excel allows you to perform numerical integration using a variety of methods, including the trapezoidal rule, Simpson's rule, and Gaussian quadrature.
• Visualization: Excel makes it easy to visualize the results of your numerical integration, which can be helpful for understanding complex systems and identifying trends.

Preparing Your Data

Before you can perform numerical integration in Excel, you'll need to prepare your data. Here are the steps to follow:

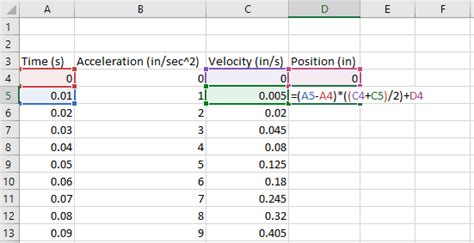
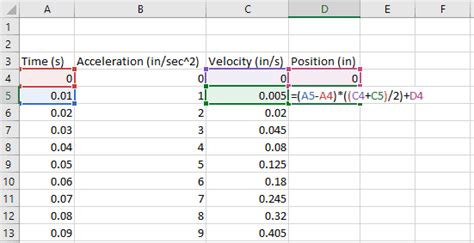
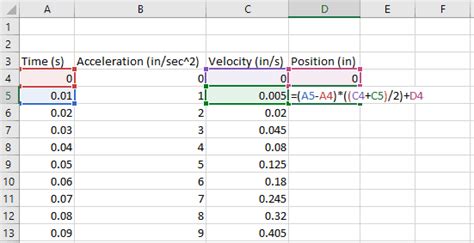
• Enter your function: Enter the function you want to integrate into a cell in your Excel worksheet. For example, if you want to integrate the function f(x) = x^2, you would enter "=x^2" into a cell.
• Create a range of x-values: Create a range of x-values that you want to use for your numerical integration. For example, if you want to integrate the function f(x) = x^2 from x=0 to x=10, you would create a range of x-values from 0 to 10.
• Calculate the corresponding y-values: Calculate the corresponding y-values for each x-value using your function. For example, if you want to integrate the function f(x) = x^2, you would calculate the y-values by squaring each x-value.

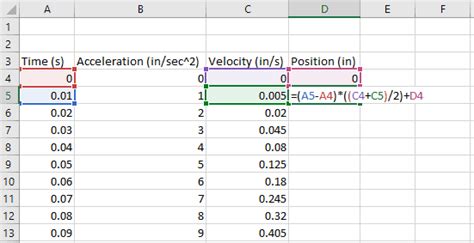
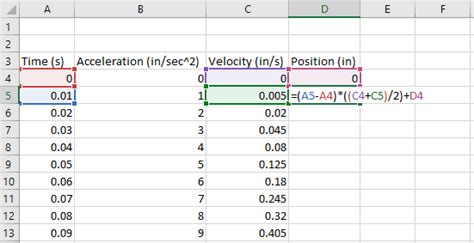
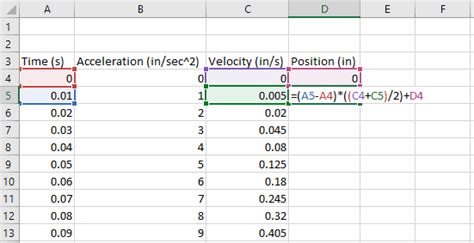
Using the Trapezoidal Rule

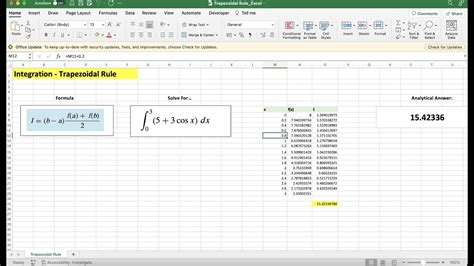
The trapezoidal rule is a simple method for approximating the value of a definite integral. Here's how to use the trapezoidal rule in Excel:

• Enter the formula: Enter the formula for the trapezoidal rule into a cell in your Excel worksheet. The formula is: =(h/2)*(f(x0) + 2*SUM(f(x1:xn-1)) + f(xn)), where h is the width of each subinterval, x0 is the lower limit of integration, xn is the upper limit of integration, and f(x) is the function being integrated.
• Calculate the result: Calculate the result of the formula to get an approximation of the definite integral.

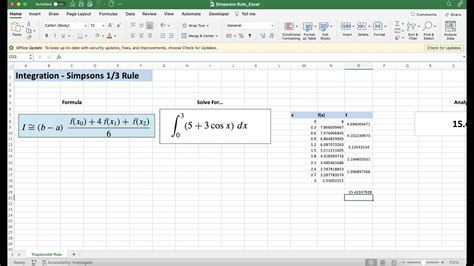
Using Simpson's Rule

Simpson's rule is another method for approximating the value of a definite integral. Here's how to use Simpson's rule in Excel:

• Enter the formula: Enter the formula for Simpson's rule into a cell in your Excel worksheet. The formula is: =(h/3)*(f(x0) + 4*SUM(f(x1:xn-1:2)) + 2*SUM(f(x2:xn-2:2)) + f(xn)), where h is the width of each subinterval, x0 is the lower limit of integration, xn is the upper limit of integration, and f(x) is the function being integrated.
• Calculate the result: Calculate the result of the formula to get an approximation of the definite integral.

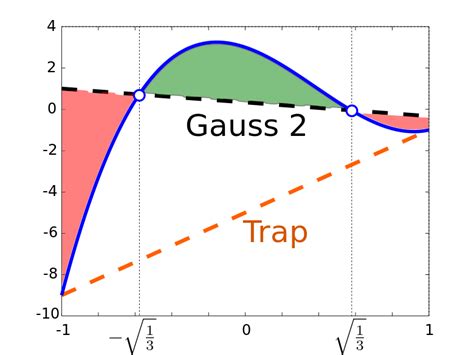
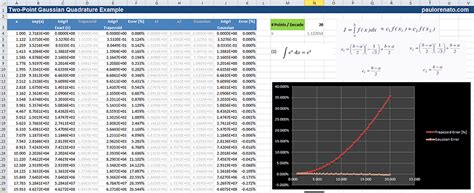
Using Gaussian Quadrature

Gaussian quadrature is a method for approximating the value of a definite integral using a weighted sum of function values at specified points. Here's how to use Gaussian quadrature in Excel:

• Enter the formula: Enter the formula for Gaussian quadrature into a cell in your Excel worksheet. The formula is: =SUM(wi*f(xi)), where wi are the weights, xi are the points, and f(x) is the function being integrated.
• Calculate the result: Calculate the result of the formula to get an approximation of the definite integral.

Tips and Variations

Here are some tips and variations to keep in mind when using numerical integration in Excel:

• Use a sufficient number of subintervals: To get an accurate result, you'll need to use a sufficient number of subintervals. The more subintervals you use, the more accurate your result will be.
• Choose the right method: The choice of method will depend on the specific problem you're trying to solve. For example, if you're integrating a smooth function, Simpson's rule may be a good choice. If you're integrating a function with a lot of oscillations, Gaussian quadrature may be a better choice.
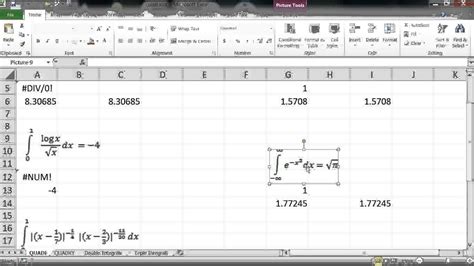
• Use Excel's built-in functions: Excel has a number of built-in functions that can be used for numerical integration, including the INT function and the SUM function.

Gallery of Numerical Integration in Excel

Numerical Integration in Excel Image Gallery

Final Thoughts

Numerical integration is a powerful tool that can be used to solve a wide range of problems in mathematics, engineering, and other fields. By following the steps outlined in this article, you can use Excel to perform numerical integration and get an approximation of the definite integral. Remember to choose the right method, use a sufficient number of subintervals, and take advantage of Excel's built-in functions to get the most accurate result.