Intro
Master trigonometry with 5 essential Trig Circle tips, covering angles, radians, sine, cosine, and tangent functions for improved math skills.
Understanding the trigonometric circle is crucial for any student of mathematics or physics. The trig circle, also known as the unit circle, is a fundamental concept that helps in solving trigonometric problems with ease. It is a circle with a radius of 1 unit, and its center is at the origin of a coordinate plane. The importance of the trig circle lies in its ability to simplify complex trigonometric calculations by providing a visual representation of angles and their corresponding trigonometric ratios.
The trigonometric circle is not just a tool for solving mathematical problems; it also has practical applications in various fields such as engineering, navigation, and physics. For instance, in engineering, the trig circle is used to design and analyze systems that involve rotational motion, while in navigation, it helps in determining directions and distances between locations. Given its wide range of applications, mastering the trig circle is essential for anyone interested in pursuing a career in these fields.
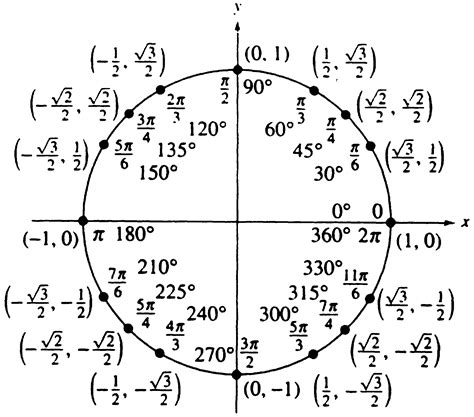
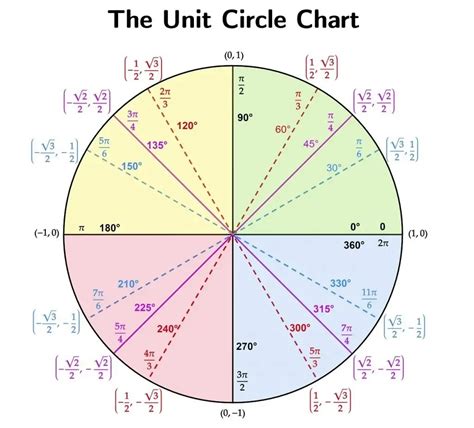
The trig circle is divided into four quadrants, each representing a different range of angles. The quadrants are numbered from I to IV, starting from the upper right and moving counterclockwise. Understanding the properties of each quadrant is vital, as it determines the sign of the trigonometric ratios. For example, in quadrant I, all trigonometric ratios (sine, cosine, and tangent) are positive, while in quadrant II, only the sine ratio is positive. This knowledge is crucial for solving trigonometric problems accurately.
Introduction to the Trig Circle
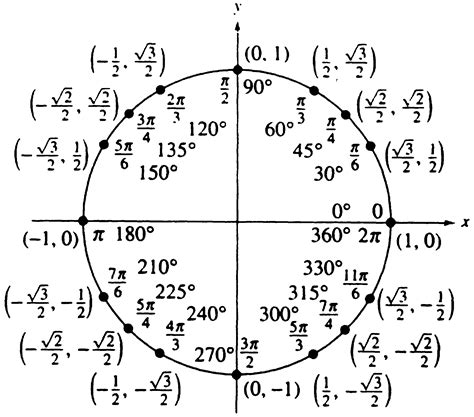
The trigonometric circle is based on the concept of a unit circle, which means that the radius of the circle is 1 unit. This simplifies calculations, as the lengths of the sides of the triangles formed within the circle can be easily determined using trigonometric ratios. The trig circle is also used to define the trigonometric functions of an angle, including sine, cosine, and tangent.
Key Components of the Trig Circle
The trig circle consists of several key components, including the radius, the center, and the quadrants. The radius is the distance from the center of the circle to any point on the circle's circumference. The center of the circle is the point from which the radius is measured, and it is usually located at the origin of a coordinate plane. The quadrants are the four sections of the circle, each representing a different range of angles.Understanding Trigonometric Ratios
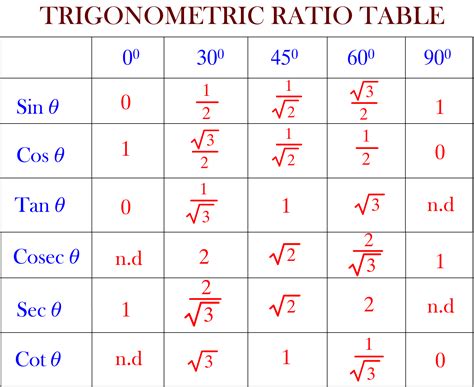
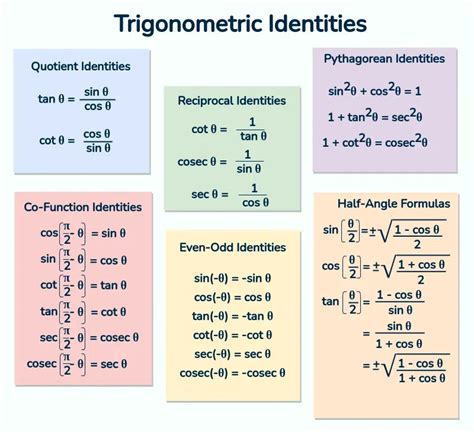
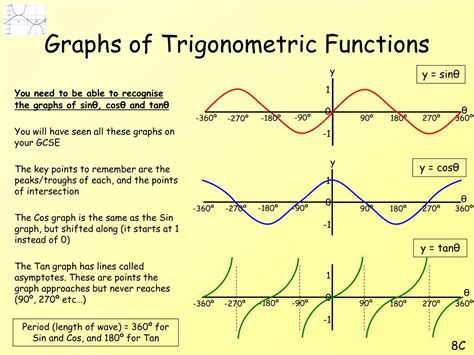
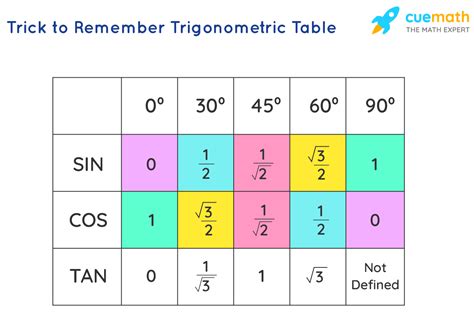
Trigonometric ratios are the foundation of the trigonometric circle. These ratios, which include sine, cosine, and tangent, are used to describe the relationships between the angles and the side lengths of triangles. The sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine of an angle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenouse. The tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Applications of Trigonometric Ratios
Trigonometric ratios have numerous applications in various fields, including physics, engineering, and navigation. In physics, trigonometric ratios are used to describe the motion of objects, including the trajectory of projectiles and the vibration of springs. In engineering, trigonometric ratios are used to design and analyze systems, including bridges, buildings, and electronic circuits. In navigation, trigonometric ratios are used to determine directions and distances between locations.Mastering the Trig Circle
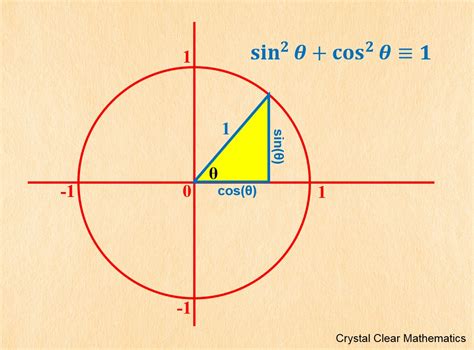
Mastering the trig circle requires practice and dedication. One of the most effective ways to master the trig circle is to practice solving trigonometric problems. These problems can range from simple calculations of trigonometric ratios to complex applications of trigonometry in physics and engineering. Another way to master the trig circle is to use visual aids, such as diagrams and graphs, to illustrate the relationships between angles and trigonometric ratios.
Tips for Mastering the Trig Circle
Here are some tips for mastering the trig circle: * Practice solving trigonometric problems regularly. * Use visual aids, such as diagrams and graphs, to illustrate the relationships between angles and trigonometric ratios. * Learn the key components of the trig circle, including the radius, the center, and the quadrants. * Understand the definitions of trigonometric ratios, including sine, cosine, and tangent. * Apply trigonometric ratios to real-world problems, including physics, engineering, and navigation.Common Mistakes to Avoid

When working with the trig circle, there are several common mistakes to avoid. One of the most common mistakes is confusing the definitions of trigonometric ratios. For example, some students may confuse the sine and cosine ratios, or they may forget that the tangent ratio is defined as the ratio of the sine to the cosine. Another common mistake is failing to consider the quadrant in which the angle lies. This can result in incorrect signs for the trigonometric ratios.
Strategies for Avoiding Mistakes
Here are some strategies for avoiding common mistakes when working with the trig circle: * Review the definitions of trigonometric ratios regularly. * Practice solving trigonometric problems in each quadrant. * Use visual aids, such as diagrams and graphs, to illustrate the relationships between angles and trigonometric ratios. * Check your work carefully to ensure that you have not made any errors.Real-World Applications of the Trig Circle

The trig circle has numerous real-world applications, including physics, engineering, and navigation. In physics, the trig circle is used to describe the motion of objects, including the trajectory of projectiles and the vibration of springs. In engineering, the trig circle is used to design and analyze systems, including bridges, buildings, and electronic circuits. In navigation, the trig circle is used to determine directions and distances between locations.
Examples of Real-World Applications
Here are some examples of real-world applications of the trig circle: * Designing a bridge: The trig circle is used to calculate the stress and strain on the bridge's supports and to determine the optimal shape of the bridge. * Analyzing the motion of a projectile: The trig circle is used to calculate the trajectory of the projectile and to determine its range and maximum height. * Determining the direction and distance between two locations: The trig circle is used to calculate the bearing and distance between the two locations.Trig Circle Image Gallery
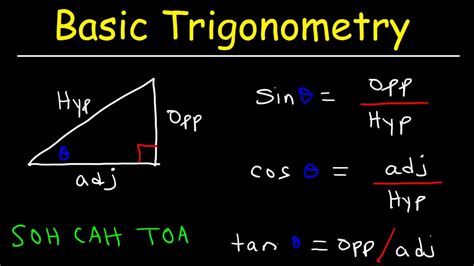




Final Thoughts

In conclusion, the trigonometric circle is a powerful tool for solving trigonometric problems and has numerous real-world applications. By mastering the trig circle, students can improve their understanding of trigonometry and develop problem-solving skills that can be applied to a wide range of fields. Whether you are a student of mathematics or physics, or an engineer or navigator, the trig circle is an essential concept that can help you achieve your goals.
We hope that this article has provided you with a comprehensive understanding of the trigonometric circle and its applications. If you have any questions or comments, please do not hesitate to share them with us. We would love to hear from you and help you in any way we can. Additionally, if you found this article helpful, please share it with your friends and colleagues who may be interested in learning more about the trigonometric circle.
